祁阳二中2007年上期高二竞赛
数学试题（问卷）
注意：本试卷共150分。考试用时120分钟.只交答卷。
一、选择题：本大题共10小题，每小题5分，共50分.）
1．设集合U=R，集合P={xx2≥x}，Q={xx>0}，则下列关系中正确的是 （ ）
A．P∩Q
Q B．P∪QQ C．P∪Q≠R D．
Q∩Q=φ
2．已知f(x)的反函数
的根为 （ ）
A．1 B．
D．2
3．设a、b表示直线，α、β表示平面，P是空间一点，下面命题正确的是 （ ）
A．a
α，则a//α B．a//α，bα，则a//b
C．α//β，aα，bα，则a//b
D．P∈a，P∈β，a//α，α//β则aβ
4．设圆x2+y2－2x+6y+1=0上有关于直线2x+y+c=0对称的两点，则c的值（ ）
A．2 B．－
5．在等差数列{an}中，若a4+a6+a8+a10+a12=120，则a9－
a11的值为 （ ）
A．14 B．
6．在△ABC中，∠C=90°，若AC=3，BC=4，则cos（A－B）的值为 （ ）
A．
B．
C．
D．
7．在平面直角坐标系中，不等式组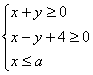
（a 为常数）表示的平面区域面积是9，那么实数a的值为 （ ）
A．3
+2
B．－3 +
|
的左
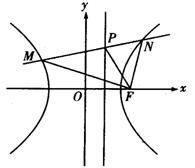
右两支分别交于M、N两点，与双曲线C的右
准线相交于P点，F为右焦点，若FM=2FN，
又
，则实数λ的取值为（ ）
A．
B．
9．平面上点P与不共线三点A、B、C满足关系式：
，则下列结论正确的是 （ ）
A．P在CA上，且
B．P在AB上，且
C．P在BC上，且
D．P点为△的重心
10．△ABC的AB边在平面α内，C在平面α外，AC和BC分别与面α成30°和45α的角，且面ABC与α成60°的二面角，那么sin∠ACB的值为 （ ）
A．1 B． C．
D．1或
二、填空题：本大题共5小题，每小题4分，共20分.
11．某校对全校男女学生共1200名进行健康调查，选用分层抽样取一个容量为200的样本，已知男生比女生多抽了10人，则该校男生人数为 人.
12．(1－x+x2)(1+x)6展开式中x3项的系数是 .
13．不等式
的解集为 .
14．一个五位数由数字0，1，1，2，3构成，这样的五位数的个数为 .
15．过定点P（1，4）作直线交抛物线C：y=2x2于A、B两点，过A、B分别作抛物线C的切线交于点M，则点M的轨迹方程为 .
祁阳二中2007年上期高二竞赛
数学试题（答卷）
一、 选择题：本大题共10小题，每小题5分，共50分.）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二、填空题：本大题共5小题，每小题4分，共20分.
11、 ；12、 ；13、 ；
14、 ；15、 。
三、解答题：本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤.
16．（本小题满分12分）
已知函数
时取到最大值.
（1）求函数f(x)的定义域；
（2）求实数 a的值.
|
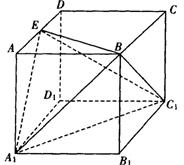
17．（本小题满分12分）如图，在边长的为1的
正方体ABCD—A1B
（1）求二面角E—A
（2）求四面体B—A
18．（本小题满分14分）
（理科做）一袋中装有分别标记着1、2、3、4数字的4个球，从这只袋中每次取出1个球，取出后放回.连续取三次，设三次取出的球中数字最大的数为ξ.
（1）求ξ=3时的概率；
（2）求ξ的概率分布列及数学期望.
（文科做）一袋中装有分别写着1，2，3，4，5数字的5个球.
（1）从袋中一次取出3个球，试求三个球中最大数字为4的概率；
（2）从这袋中每次取出1个球，取出后放回，连续三次，试求取出的三个球中最大数字为4的概率.
19．（本小题满分14分）
已知直线
交于P、Q两点，以PQ为直径的圆过椭圆C的右顶点A.
（1）设PQ中点
（2）求椭圆C方程.
20．（本小题满分12分）
已知函数
（1）当b=0时，若f（x）在[2，+∞]上单调递增，求a的取值范围；
（2）当a为整数时，若存在x0是f（x）的最大值，g（x0）是 g（x）的最小值，求a，b的值
21．（本小题满分14分）
（文科做）设数列
（1）求数列
的通项公式
；
（2）求数列
的前n项和
.
（理科做）已知点
（1）求f(x)的定义域；
（2）求证：
；
（3）求证：数列{an}前n项和
参考答案
一、选择题.
AADDC CDAAD
二、填空题。
11．630 12.11 13.
14.48 15.y=4x－4
三、解答题
16．解：（1）x要满足cos2x≠0，从而
，
因此f(x)的定义域为
……………………（4分）
（2）由
…………（4分）
求得a=－4…………………………（12分）
因此所求实数a的值为－4.
|
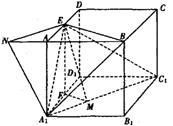
E为AD中点，在A1D1上取中点F.连接EF过FW和
FM⊥A
二面角E—A1C1—D1的平面角.
在△A1C1D1中，FM=
，
又EF⊥FM，EF=1
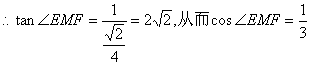
∴二面角E—A1C1—D1的余弦值为.………………………………（6分）
（2）在平面ABCD内，延长BA至N点，使AN=，故NE//A
∴NE//面BA
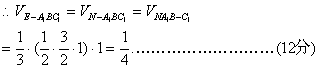
18．（理科）解：（1）ξ=3表示取出的三个球中 数字最大者为3.
①三次取球均出现最大数字为3的概率P1=（
）3
②三次取球中有2次出现最大数字3的概率
③三次取球中仅有1次出现最大数字3的概率
.…………………………（6分）
（2）在ξ=k时，利用（1）的原理可知：
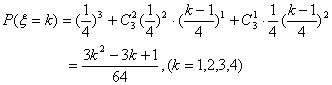
ξ的概率分布为：
| ξ | 1 | 2 | 3 | 4 |
| P |
|
|
|
|
Eξ=1×
+2×
+3×
+4×
=
.……………………（12分）
（文科）解：（1）从袋中一次取出3个球，其中数字最大为4时的概率，
…………5分
（2）从袋中每次取出1个球，取出后立刻放回，连续取三次。
①三次都取到4时概率
②三次中有2次取到4时的概率
③三次中有1次取到4时的概率
因此取出的三次球中，最大数字为4的概率
…………12分
19．解：（1）设直线交于P(x1，y1)，
Q（x2，y2），右顶点A（a，0）
将
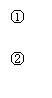于是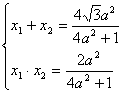
∵M（x0，y0）为PQ中点
………………（5分）
（2）依题意：
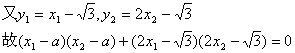
整理得：5x1x2－(2
+a)(x1+x2)+a2+3=0……………………③
由①②代入③得：a3－a2+3=0
∴(a－)(4a3－a－)=0
∵a>1 则4a3－a－>0，故a=
故所求椭圆方程为
………………………………（12分）
20．（1）当b=0时，f（x）=ax2－4x
若
上递减，f（x）=－4x，则f（x）在上递减，不合题意。……3分
则a≠0，要使f（x）在上递增，则a≥1……………………………………6分
（2）若上递减，
无最大值
知a≠0，要使f（x）有最大值，必须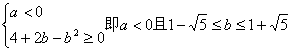
此时
取最大值，
又g（x）取最小值时，x=x0=a时依题意有
又a＜0，a∈Z，则a=－1，此时b=－1或3。………………12分
21．解：（1）由
故x>0或x≤－1
f(x)定义域为
…………………………（4分）
（2）（理科）
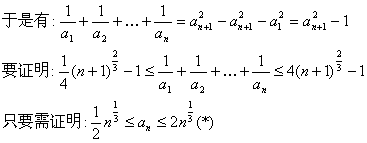
下面使用数学归纳法证明：
①在n=1时，a1=1，<a1<2，则n=1时（*）式成立.
②假设n=k时
成立，
由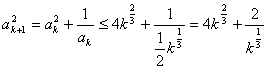
要证明：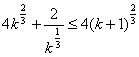
只需
只需(2k+1)3≤8k(k+1)2
只需1≤4k2+2k
而4k2+2k≥1在k≥1时恒成立.
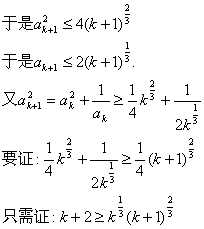
只需证：4k2+11k+8>0，而4k2+11k+8>0在k≥1时恒成立.
于是：
因此
得证.
综合①②可知（*）式得证.从而原不等式成立.………………（9分）
（3）要证明：
由（2）可知只需证：
…………（**）
下面用分析法证明：（**）式成立。
要使（**）成立，只需证：
即只需证：(3n－2)3n>(3n－1)3(n－1)
只需证：2n>1
而2n>1在n≥1时显然成立.故（**）式得证：
于是由（**）式可知有：
因此有：
……………………………………（14分）
（文科）．解：（1）
的前n项和
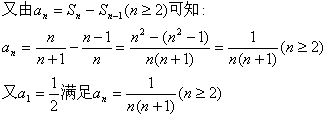
故数列
…………6分
（2）
于是的前n项之和
…………12分
欢迎访问 http://www.k12zy.com