上海交通大学附属中学2007-2008学年度第一学期
高二数学期中试卷
本试卷共有22道试题，满分100分，考试时间90分钟。
请考生用钢笔或圆珠笔将答案写在答题卷上
（本试卷允许使用计算器。凡属用计算器所得之值，请精确到小数点后3位）
命题：侯磊 审核：杨逸峰
一、填空题（本大题满分36分）本大题共有12题，只要求直接填写结果，每个空格填对得3分，否则一律得零分。
1、
已知矩阵
，
，则2A－3B=_________________。
2、
已知
，
，则
_________________。
3、
已知向量
=(k,1)，
=(1,0)，△ABC是直角三角形，则k=___________。
4、
已知向量
和
夹角为120°，且=2=5，则（2－）·=___________。
5、
已知点P分有向线段
的比是2，则P2分有向线段
所成的比是
。
6、
为非零向量，
，
，且
，则四边形ABCD的形状是
。
7、
由
，
，
，…
可得的归纳猜想是___________________________。
8、
若
，则
__________________。
9、
设数列
的前n项和为
，则下列命题中正确的是______（填写正确命题的编号）。
（1） 
，则为等差数列；
（2） 数列为等差数列，则必存在实数
使得
；
（3） 为等差数列，则数列
为等比数列；
（4）
为等比数列，且
，则
10、用数学归纳法证明“1+
+
+…+
＜n（n∈N*，n＞1）”时，由n=k（k＞1）不等式成立，推证n=k+1时，左边应增加的项数是
。
11、已知
、
为两个非零向量，有以下命题：①
=
，②·=，③=且∥，以其中两个为条件，一个为结论的真命题有_________个。
12、对n个向量，若存在n个不全为零的实数k1，k2，……，kn，使得＝0，则称向量是“线性相关”的，按此规定，能说明平面向量
，
，
“线性相关”的实数k1，k2，k3依次可以取____________。
二、选择题（本大题满分12分）本大题共有4题，每题都给出代号为(A)、(B)、(C)、(D)的四个结论，其中有且只有一个结论是正确的，必须把正确结论的代号写在对应的空格内，选对得3分，不选、选错或者选出的代号超过一个（不论是否都写在空格内），一律得零分。
13、在100和200之间能被3整除的所有数的和是 ( )
(A) 4950 (B) 9900 (C) 4800 (D) 9600
14、下列命题正确的是 ( )
(A) 向量与
是平行向量，则直线AB与CD平行
(B) 设A、B、C、D是某个四边形的四个顶点，则这个四边形是平行四边形的充要条件是=
(C) 非零向量与平行，则与方向相同或相反
(D) 单位向量都相等
15、G为△ABC内一点，且满足
，则G为△ABC的 ( )
(A) 外心 (B) 内心 (C) 垂心 (D) 重心
16、数列满足递推公式
，则下列叙述正确的是 ( )
(A) 数列是单调递增数列 (B) 数列极限必不存在
(C) 数列的前n项和Sn=2n (D) 以上都不对
三、解答题（本大题满分52分）本大题共有6小题，解答下列各题必须写出必要的步骤。
17、（本题满分6分）已知矩阵
，
，
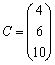，求：(AB)C和(3A-2C)B。
18、（本题满分8分）数列{an}的前n项和Sn=n2-7n-8，
（1） 求数列{an}的通项公式；
（2） 数列{an}的前n项和Tn。
19、（本题满分8分）已知数列{an}是等比数列，首项a1＝8，公比q>0，令bn＝log2an，设Sn为{bn}的前n项和，若数列{bn}的前7项的和S7最大，且S7≠S8，求数列{an}的公比q的取值范围。
20、（本题满分10分）已知向量
=（2，1），
=（1，7），
=（5，1），设X是直线OP上的一点（O为坐标原点），求
的最小值及取到最小值时X点的坐标。
21、（本题满分10分）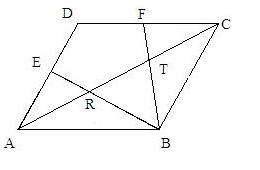
如图,连接平行四边形ABCD的一个顶点B与AD、DC边的中点
E、F, BE、BF分别与AC交于R、T两点,
（1）设
，
，
，试用，和
表示
、
（不需要求出）
（2）求证：AR=RT=TC。
22、（本题满分10分）已知二次项系数为正的二次函数
对任意
，都有
成立，设向量
（sinx，2），
（2sinx，
），
（cos2x，1），
（1，2），当
[0，
]时，求不等式f（
）＞f（
）的解集。