高二数学期末复习5

高二数学期末复习训练（圆锥曲线②）2002.6

1．抛物线y=2x²的焦点坐标是（　）.

　（A）(1, 0)　（B）(, 0)　（C）(0,)　（D）(0,)

2．双曲线的焦距等于双曲线的两条准线间距离的2倍，则双曲线的离心率是（　）.

　（A）　　（B）　　（C）2　　（D）3

3．如果抛物线的顶点在原点，对称轴为x轴，焦点在直线3x－4y－12=0上，则抛物线的方程是（　）.

　（A）y²=12x　 （B）y²=－12x 　（C）y²=16x　 （D）y²=－16x

4．设正三角形的三个顶点都在抛物线y²=4x上，正三角形的一个顶点是坐标原点，这个正三角形的面积是（　）.

　（A）48　（B）24　（C）　（D）46

5．过抛物线y²=2x的焦点F的直线与抛物线交于A(x₁, y₁)、B(x₂, y₂)两点，若x₁＋x₂=3，则AB等于（　）.

　（A）2　　（B）3　　（C）4　　（D）5

6．椭圆(1－m)x²－my²=1的长轴长是　　　　　　　　　　　　　　　 （　）

（A）　　（B）　　（C）　　（D）

7．椭圆的两个焦点和中心把两准线间的距离四等分，则一焦点与短轴两端点连线的夹角是　　　　　　　　　　　　　　　　　　　　　　　　　  （　）

  （A）　　  （B）　　  （C）　　　 （D）

8．已知椭圆的左顶点在直线上,则

　 (A)2　　　　　 (B)1　　　　　 (C)－1　　　　 (D)－2

9. 已知直线及点P(1,0),若P点关于l的对称点在双曲线上,则双曲线的焦点坐标是(　　)

　(A)　　(B) 　　(C) 　　(D)

10.与双曲线有共同渐近线,且经过点的双曲线的共轭双曲线的方程是(　 )

　(A)　(B) 　(C) 　(D)

11.椭圆的焦点为F₁和F₂,点P在椭圆上,如果线段F₁P的中点在y轴上,那么PF₁是PF₂的(　　)

(A)７倍　　　(B)５倍　　　　(C)４倍　　　　　(D)３倍

12.若直线与双曲线的右支有两个不同的交点,则k的取值范围是(　)

　 (A)　　 (B) 　　　(C) 　　(D)

13.曲线C:与直线有且仅有一个公共点,则k=_______.

14.直线l过定点(－2,0),且与抛物线交于A、B两点,若P为线段AB的中点,则直线l的方程是_______________________.

15. 椭圆的离心率为,则a=_________

16. 某桥的桥洞呈抛物线形,桥下水面宽16m,当水面上涨2m后达到警戒水位,水面宽变为12m,此时桥洞顶距水面高度为___________(精确到0.1)

17．如图所示,已知A、B是两个定点,且,动点M到点A的距离是4,线段MB的垂直平分线L交MA于点P.

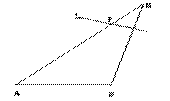⑴当M变化时,建立适当的坐标系,求动点P的轨迹方程,并说明轨迹表示什么图形.

 ⑵设点Q是⑴中轨迹上的点,且,求的值.

18. 抛物线上存在弦AB被直线垂直平分,求实数a的取值范围.

　 19.已知圆C₁的方程为椭圆C₂的方程为(a>b>0),C₂

的离心率为如果C₁与C₂相交于A、B两点，且AB恰好为圆C₁的直径，求直线AB的方程和椭圆C₂的方程.

20.A、B、C三点是我方三个炮兵阵地，A在B的正东，距B6千米；C在B的北偏西30^O，距B4千米；P点为敌炮兵阵地.某时刻A发现敌炮兵阵地的某种信号（已知该信号的传播速度是1千米/秒，　　　　　　　 若A炮击P地，求炮击的方位角和距离.

　　21．已知圆的圆心为M₁，圆的圆心为M₂，一动圆与这两圆都外切.（1）求动圆圆心P的轨迹方程；（2）若过M₂的直线与（1）中的轨迹交于两点A、B，求的取值范围.

22. 已知椭圆的一个顶点为A（0，－1），焦点在x轴上，若右焦点到直线x－y+2=0的距离为3.

(1) 求椭圆的方程；

　 （2）设椭圆与直线y=kx+m(k≠0)相交于不同的两点M、N，当AM=AN时，求m的取值范围.

23.设双曲线C₁:的离心率为e,右准线L与两渐近线交于P、Q两点,右焦点为F,且ΔPQF为等边三角形.以F为左焦点,L为左准线的椭圆C₂的短轴端点为B.　⑴若双曲线C₁被直线截得弦长是,试求双曲线C₁的方程;

⑵若双曲线C₁过点(1,0),试求离心率为的椭圆C₂的方程;

⑶若双曲线C₁过点(1,0),求BF中点的轨迹方程.