2007年下学期长沙市实验中学高二期中考试数学试题
高 班 姓名 记分
一、选择题:(本题共10小题,每题5分,共50分,每小题有且仅有一个答案正确)
1、若![]() ,则下列不等式中成立的是
( )
,则下列不等式中成立的是
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2. 不等式![]() 的解集是( )
的解集是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、不等式![]() 的取值范围是
的取值范围是
( )
![]()
4.直线Ax+By+C=0右侧的点(x0, y0),则Ax0+By0+C的值( )
(A)与A同号 (B)与A异号 (C)与B同号 (D)与B异号
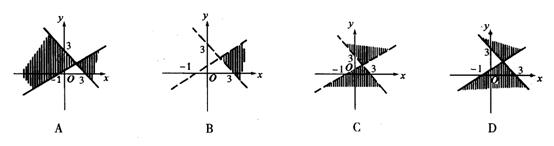
5.如图所示,不等式(x–2y+1)(x+y–3)<0表示的平面区域是( )
6.圆![]() 关于直线
关于直线![]() 对称的圆的方程是( )
对称的圆的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7、如果l1,l2的斜率分别是二次方程x2-4x+1=0的两根,则l1,l2的夹角是( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
8、直线l1:ax-y-b=0,l2:bx-y+a=0(ab≠0,a≠b),下列图形中正确的是 ( )
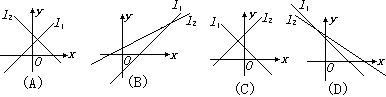
9、已知三条直线为l1: x-2y+4a=0, l2: x-y-6a=0, l3: 2x-y-4a=0 ![]() , 则下列结论中正确的一个是
( )
, 则下列结论中正确的一个是
( )
(A) 三条直线的倾斜角之和为900. (B) 三条直线在y轴上的截距b1, b2,b3满足b1+b3=2b2.
(C) 三条直线的倾斜角α1,α2,α3满足α1+α3=2α2.
(D) 三条直线在x轴上截距之和为12a.
10、将直线![]() 绕(1,0)点顺时针旋转90°后,再向上平移1个单位与圆
绕(1,0)点顺时针旋转90°后,再向上平移1个单位与圆![]() 相切,则r的值是
( )
相切,则r的值是
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)1
(D)1
二.填空题:(本大题共5小题,共25分。)
11.求z=![]() x+2y的最大值,使式子中的x, y满足
x+2y的最大值,使式子中的x, y满足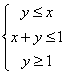 的问题中,不等式组叫做的
,z=
的问题中,不等式组叫做的
,z=![]() x+2y叫做
。
x+2y叫做
。
12、三条直线x+y+1=0,2x-y+8=0和ax+3y-5=0只有两个不同的交点,则a=____________
13、过点M(0,4)、被圆![]() 截得的线段长为
截得的线段长为![]() 的直线方程为
的直线方程为
14、方程![]() 表示的图形是半径为
表示的图形是半径为![]() (
(![]() )的圆,则该圆圆心在第 象限
)的圆,则该圆圆心在第 象限
15.已知两条直线![]() 和
和![]() 互相垂直,则
互相垂直,则![]() =
=
三、解答题(本大题共6小题,共75分。)
16.(本小题满分12分)
解不等式![]() >0.
>0.
17、(本小题满分12分)
一直线被两直线l1:4x+y+6 = 0,l2:3x-5y-6 = 0截得的线段的中点恰好是坐标原点,求直线的方程。
18.(本小题满分12分)
设变量![]() 、
、![]() 满足约束条件
满足约束条件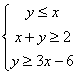 ,在坐标系中画出可行域,并且求目标函数
,在坐标系中画出可行域,并且求目标函数![]() 的最小值。
的最小值。
19、(本小题满分13分) 设![]()
20、(本小题满分13分)
已知过两定点的一个交点O的动直线与两圆分别交于点A、B,求线段AB中点P的轨迹方程。
21、(本小题满分13分)
甲、乙两地生产某种产品,它们可调出的数量分别为300t和750t,
A、B、C三地需要该种产品的数量分别为200t、450t和400t.甲地运往A、B、C三
地的运费分别为6元/t、3元/t、5元/t;乙地运往A、B、C三地的运费分别为5元/t、
9元/t、6元/t.问怎样的调运方案,才能使总运费最省?
2007年下学期长沙市实验中学高二期中考试数学试题答案
一、选择题:(本题共10小题,每题5分,共50分,每小题有且仅有一个答案正确)
1、若![]() ,则下列不等式中成立的是
( )C
,则下列不等式中成立的是
( )C
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2. 不等式![]() 的解集是( D )
的解集是( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、不等式![]() 的取值范围是
的取值范围是
( )C
![]()
4.直线Ax+By+C=0右侧的点(x0, y0),则Ax0+By0+C的值( )A
(A)与A同号 (B)与A异号 (C)与B同号 (D)与B异号
5.如图所示,不等式(x–2y+1)(x+y–3)<0表示的平面区域是( )C

6.圆![]() 关于直线
关于直线![]() 对称的圆的方程是( )C
对称的圆的方程是( )C
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7、如果l1,l2的斜率分别是二次方程x2-4x+1=0的两根,则l1,l2的夹角是( )C
A ![]() B
B ![]() C
C ![]() D
D ![]()
8、直线l1:ax-y-b=0,l2:bx-y+a=0(ab≠0,a≠b),下列图形中正确的是 ( ) B
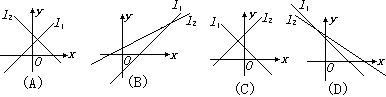
9、已知三条直线为l1: x-2y+4a=0, l2: x-y-6a=0, l3: 2x-y-4a=0 ![]() , 则下列结论中正确的一个是
( ) C
, 则下列结论中正确的一个是
( ) C
(A) 三条直线的倾斜角之和为900. (B) 三条直线在y轴上的截距b1, b2,b3满足b1+b3=2b2.
(C) 三条直线的倾斜角α1,α2,α3满足α1+α3=2α2.
(D) 三条直线在x轴上截距之和为12a.
10、将直线![]() 绕(1,0)点顺时针旋转90°后,再向上平移1个单位与圆
绕(1,0)点顺时针旋转90°后,再向上平移1个单位与圆![]() 相切,则r的值是
( ) A
相切,则r的值是
( ) A
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)1
(D)1
二.填空题:(本大题共5小题,共25分。)
11.求z=![]() x+2y的最大值,使式子中的x, y满足
x+2y的最大值,使式子中的x, y满足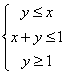 的问题中,不等式组叫做的
,z=
的问题中,不等式组叫做的
,z=![]() x+2y叫做
。(线性约束条件、线性目标函数)
x+2y叫做
。(线性约束条件、线性目标函数)
12、三条直线x+y+1=0,2x-y+8=0和ax+3y-5=0只有两个不同的交点,则a=____________
3或-6
13、过点M(0,4)、被圆![]() 截得的线段长为
截得的线段长为![]() 的直线方程为
的直线方程为
3、x=0或15x+8y-32=0(写出一个方程给2分)
14、方程![]() 表示的图形是半径为
表示的图形是半径为![]() (
(![]() )的圆,则该圆圆心在第 象限 ( 四 )
)的圆,则该圆圆心在第 象限 ( 四 )
15.(福建卷)已知两条直线![]() 和
和![]() 互相垂直,则
互相垂直,则![]() =
=
![]()
解析:两条直线![]() 和
和![]() 互相垂直,则
互相垂直,则![]() ,∴ a=-1,
,∴ a=-1,
三、解答题(本大题共6小题,共75分。)
16.(本小题满分12分)
解不等式![]() >0.
>0.
解:因为对任意![]() ,
,![]() ,所以原不等式等价于
,所以原不等式等价于![]() .
.
即![]() ,
,![]() ,
,![]() ,故解为
,故解为![]() .
.
所以原不等式的解集为![]() .
.
17、(本小题满分12分)
一直线被两直线l1:4x+y+6 = 0,l2:3x-5y-6 = 0截得的线段的中点恰好是坐标原点,求直线的方程。
17、解:设线段MN, M(x0,y0),
N(-x0,-y0),
M![]() l1, N
l1, N![]() l2,
l2,
∴4x0+y0+6 = 0 (1) -3x0+5y0-6 = 0 (2),
(1)-(2) 得x0+6y0 = 0 ∴M,N在直线x+6y = 0上,又过原点,即所求.
 18.(本小题满分12分)设变量
18.(本小题满分12分)设变量![]() 、
、![]() 满足约束条件
满足约束条件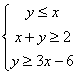 ,在坐标系中画出可行域,并且求目标函数
,在坐标系中画出可行域,并且求目标函数![]() 的最小值。
的最小值。
18、解析:设变量![]() 、
、![]() 满足约束条件
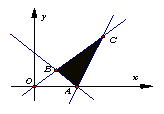
满足约束条件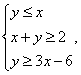 在坐标系中画出可行域△ABC,A(2,0),B(1,1),C(3,3),则目标函数
在坐标系中画出可行域△ABC,A(2,0),B(1,1),C(3,3),则目标函数![]() 的最小值为3。
的最小值为3。
19、(本小题满分13分) 设![]()
19、解:![]()
![]()
![]() 即
即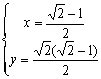 时取等号,
时取等号,
![]()
![]()
20、(本小题满分13分)
已知过两定点的一个交点O的动直线与两圆分别交于点A、B,求线段AB中点P的轨迹方程。
20、 如图,以O为原点,建立平面直角坐标系
因为两定圆均过原点O,故可设其方程分别 为:x2+y2-2ax-2by=0 ①
x2+y2-2cx-2dy=0 ②
当动直线斜率存在时,设其方程为
y=kx ③
将方程③分别与方程①、②联立,可得
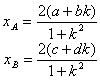
设线段AB的中点为P(x,y),则
![]() ④
④
∵点P在直线y=kx上
∴将![]() 代入④,消去k,得:
代入④,消去k,得: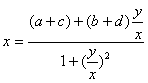
整理得:x2+y2-(a+c)x-(b+d)y=0 ⑤
当动直线斜率不存在时,其方程为:x=0,分别代入①、②可得A(0,2b),B(0,2d)
则AB的中点P为(0,b+d),将此代入⑤式,仍成立。
∴所求动点P的轨迹方程为 x2+y2-(a+c)x-(b+d)y=0
21、(本小题满分13分)甲、乙两地生产某种产品,它们可调出的数量分别为300t和750t,
A、B、C三地需要该种产品的数量分别为200t、450t和400t.甲地运往A、B、C三
地的运费分别为6元/t、3元/t、5元/t;乙地运往A、B、C三地的运费分别为5元/t、
9元/t、6元/t.问怎样的调运方案,才能使总运费最省?
解:21.设由甲地调往A、B两地的产品数量各为xt,yt,则甲地调往C地为![]() ,所以乙地调
,所以乙地调
往A、B、C三地的产量数量分别为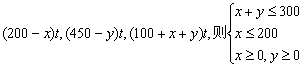 ,
,
目标函数
![]() …8分
…8分
作出可行域,平移直线![]() 可知过点(0,300)时,
可知过点(0,300)时,![]() ,
,
所以甲地的产品全部运往B地,乙地的产品运往A、B、C三地分别为200t,150t,400t时总运费最省为5650元…13分