2007学年奉贤区调研测试高二数学试卷
(完卷时间90分钟,满分100分) 08.1
一、 填空题(本大题满分33分,每题3分,)
1、 在数列![]() 中,
中,![]() ,则
,则![]()
2、已知直线l经过P(-1,-1)、Q(2,2)两点,则直线l的倾斜角为
3、行列式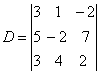 中元素7的代数余子式是
.
中元素7的代数余子式是
.
4、若直线![]() 经过点
经过点![]() 且与向量
且与向量![]()
![]() 平行,则直线
平行,则直线![]() 的一般式方程为______________
的一般式方程为______________
5、若数列![]() 满足:
满足:![]() 且对任意正整数
且对任意正整数![]() ,都有
,都有![]() ,则
,则![]() (
(![]() +
+![]() +···+
+···+![]() )=
)=
6、已知正方形![]() 的边长为1,则
的边长为1,则![]() =
=
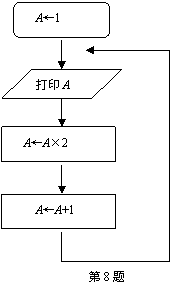 7、已知矩阵
7、已知矩阵![]()
![]()
![]() ,
,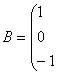
![]() ,则
,则![]()
8、根据框图,写出所打印数列![]() 的
的
递推公式
9、不等式![]()
![]() 的解集是___________
的解集是___________
10、已知向量![]() =(1, 1),若
=(1, 1),若![]() 与非零向量
与非零向量![]() +2
+2 ![]() 方向相同,
方向相同,
则![]() ·
·![]() 的范围是
的范围是
11、已知数列![]() 的通项公式为:
的通项公式为:![]() =
=![]() +
+![]() n-25,(n
n-25,(n![]()
![]() ),
),![]() 是表示数列
是表示数列![]() 的前n项和,则
的前n项和,则![]() 的最小值为
。
的最小值为
。
二、选择题(本大题满分16分。每题4分,)
12、三阶行列式的两行成比例是这个行列式的值为零的( )
(![]() )充分非必要条件
(
)充分非必要条件
(![]() )必要非充分条件
)必要非充分条件
(![]() )充要条件
(
)充要条件
(![]() )非上述答案
)非上述答案
13、对于向量![]() 和实数
和实数![]() ,下列命题中真命题是( )
,下列命题中真命题是( )
(![]() )若
)若![]() ,则
,则![]() 或
或![]()
(![]() )若
)若![]() ,则
,则![]() 或
或![]()
(![]() 若
若![]() ,则
,则![]() 或
或![]()
(![]() )若
)若![]()
![]() ,则
,则![]()
14、某人为了观看2008年奥运会,从2001年起,每年8月8日到银行存入![]() 元定期储蓄,若年利率为
元定期储蓄,若年利率为![]() 且保持不变,不计利息税,并约定每年到期存款均自动转为新的一年定期,到2008年8月8日将所有的存款及利息全部取回,则可取回的钱的总数(元)为
( )
且保持不变,不计利息税,并约定每年到期存款均自动转为新的一年定期,到2008年8月8日将所有的存款及利息全部取回,则可取回的钱的总数(元)为
( )
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]()
15、算法:第一步 ![]() ;第二步 若
;第二步 若![]() 则
则![]() ;第三步 若
;第三步 若![]() ,则
,则![]() ; 第四步 若
; 第四步 若![]() ,则
,则![]() ; 第五步 输出
; 第五步 输出![]() . 则输出的
. 则输出的![]() 表示( )
表示( )
(![]() )
)![]() 中的最大值;
(
中的最大值;
(![]() )
)![]() 中的最小值
中的最小值
(![]() )将
)将![]() 由小到大排序 (
由小到大排序 (![]() )将
)将![]() 由大到小排序
由大到小排序
三、解答题(本大题共有5题,满分51分,解答下列各题必须写出必要的步骤)
16.(本题满分8分,第1小题4分,第2小题4分)
已知![]() ∥
∥![]()
(1)求![]() 的值;
的值;
(2)求与![]() 同向的单位向量
同向的单位向量
解:
17.(本题满分8分,第1小题4分,第2小题4分)
已知某小区1号楼、2号楼在2007年1月、2月内两幢楼的水、电、煤用量分别如下表所示:
表1(1月份)
|
楼号 | 用水量(m3) | 用电量(kw/h) | 用煤气量(m3) |
| 1号楼 | 1300 | 243 | 349 |
| 2号楼 | 1121 | 201 | 371 |
表2(2月份)
|
楼号 | 用水量(m3) | 用电量(kw/h) | 用煤气量(m3) |
| 1号楼 | 1633 | 349 | 417 |
| 2号楼 | 1248 | 288 | 279 |
如果每单位量的水费、电费、煤气费分别为1.03元、0.60元、1.05元,试解决以下问题:
(1) 将两幢楼的水、电、煤气在上述两个月的总用量用一个矩阵表示;
(2) 已知两幢楼的水、电、煤气在2007年3月份的用量比2007年2月份的用量减少10%,将两幢楼的水、电、煤气在2007年3月份的用量用一个矩阵表示;
解:
18、(本题满分10分,第1小题4分,第2小题6分)
已知等比数列![]() 的首项
的首项![]() =1,公比为
=1,公比为![]()
(1)求二阶行列式![]() 的值;
的值;
(2)试就![]() 的不同取值情况,讨论二元一次方程组
的不同取值情况,讨论二元一次方程组![]() 何时无解,何时有无穷多解?
何时无解,何时有无穷多解?
解:
19、(本题满分12分,第1小题5分,第2小题7分)
在平面直角坐标系中,已知点A(1,3)、B(4,1),直线![]() 方程为:2x+3y-3=0
方程为:2x+3y-3=0
(1)、若直线![]() 与x轴正半轴交于P点,求
与x轴正半轴交于P点,求![]() 的面积
的面积
(2)、请在直线![]() 上另取一点
上另取一点![]() ,求出
,求出![]() 的面积,根据
的面积,根据![]() 和
和![]() 的面积关系,你能进一步猜想出更一般的结论吗?并证明你的结论。
的面积关系,你能进一步猜想出更一般的结论吗?并证明你的结论。
解:
20、(本题满分13分,第1小题4分,第2小题4分,第3小题5分)
设数列![]() 是公差不为零的等差数列,
是公差不为零的等差数列,![]() =6
=6
(1)当![]() =3时,请在等差数列
=3时,请在等差数列![]() 中找一项
中找一项![]() ,使
,使![]() 成等比数列;
成等比数列;
(2)当![]() =2 时,若自然数
=2 时,若自然数![]()
![]()
![]() ,···满足5<
,···满足5< ![]() <
<![]() <··· <
<··· <![]() <
···
<
···
且![]()
![]()
![]()
![]() ,···是等比数列.求
,···是等比数列.求![]() (用t表示);
(用t表示);
(3)若存在自然数![]()
![]()
![]() ,···满足5<
,···满足5< ![]() <
<![]() <··· <
<··· <![]() <
···且
<
···且
![]()
![]()
![]()
![]() ,···构成一个等比数列,求证:整数
,···构成一个等比数列,求证:整数![]() 必是12的一个正约数
必是12的一个正约数
解:
2007学年奉贤区高二数学调研试卷参考答案
二、 填空题(本大题满分33分,每题3分,)
2、 11 2、![]() 3、
3、![]() 4、
4、![]() 5、
5、![]() 6、1 7、
6、1 7、![]()
![]()
8、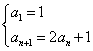 9、
9、![]() 10、(-1,+∞) 11、
10、(-1,+∞) 11、![]() 3-67
3-67
二、选择题(本大题满分16分。每题4分,)
12、(A) 13、(B) 14、(
D ) 15、(![]() )
)
三、解答题(本大题共有5题,满分51分,解答下列各题必须写出必要的步骤)
16.(本题满分8分,第1小题4分,第2小题4分)
解:(1)∵![]() ,∴
,∴![]() ,
(2分)
,
(2分)
解方程得:![]() 或
或![]() 。
(2分)
。
(2分)
(2)当![]() 时
时![]() ,
,![]() ,则
,则![]() ;
(2分)
;
(2分)
当![]() 时
时![]() ,
,![]() ,则
,则![]() 。
(2分)
。
(2分)
17.(本题满分8分,第1小题4分,第2小题4分)
(1)设两个月的总用量为矩阵![]() ,则:A=
,则:A=![]() .
(4分)
.
(4分)
(2)设2007年3月份的用量对应的矩阵B,则:
B=![]() .
(4分)
.
(4分)
18、(本题满分10分,第1小题4分,第2小题6分)
解:(1)![]() =
=![]()
![]() -
-![]()
![]() =0
(4分)
=0
(4分)
(2)D= ![]() =0,
(1分)
=0,
(1分)
![]() =
=![]() =
=![]() (3q+2),
(1分)
(3q+2),
(1分)
![]() =
=![]() =-(3q+2),
(1分)
=-(3q+2),
(1分)
当![]() 时,
时,![]() ,原方程组有无穷多解;
(2分)
,原方程组有无穷多解;
(2分)
当![]() 时,
时,![]() ,但
,但![]() 0,所以原方程组无解
(1分)
0,所以原方程组无解
(1分)
19、(本题满分12分,第1小题5分,第2小题7分)
解:(1)点![]() ,
(1分)
,
(1分)
![]() 。(方法有点到直线距离公式和三阶行列式面积公式二种)
(4分)
。(方法有点到直线距离公式和三阶行列式面积公式二种)
(4分)
(2)
当M为直线![]() 上任意点时,
上任意点时,![]() =
=![]() (2分)
(2分)
由![]() ,
,
结论:当M为直线![]() 上任意点时,
上任意点时,![]() 的面积是定值为
的面积是定值为![]() (2分)
(2分)
因为直线![]() 的方程是
的方程是![]() 与直线
与直线![]() 平行,所以直线
平行,所以直线![]() 上任意点
上任意点![]() 到
到![]() 的距离相等,则
的距离相等,则![]() 的面积是个定值为
的面积是个定值为![]() 。 (3分)
。 (3分)
20、(本题满分13分,第1小题4分,第2小题4分,第3小题5分)
解:(1)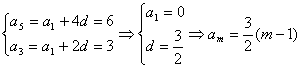 ,
(2分)
,
(2分)
又因为![]() 成等比数列,所以
成等比数列,所以![]() ,
,![]() ,即
,即![]() 中的
中的![]() (2分)
(2分)
(2)∵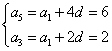 解得
解得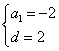 ,∴
,∴![]() ,
(2分)
,
(2分)
∴![]() ,
,
又∵![]() ,∴
,∴![]() ;
(2分)
;
(2分)
(3)因为![]()
,所以![]() , (1分)
, (1分)
因为![]() 成等比数列,
成等比数列,
所以![]() (2分)
(2分)
因为![]() 所以
所以![]() (舍),
(舍),
故整数![]() 必是12的一个正约数
(2分)
必是12的一个正约数
(2分)
 用量 项目
用量 项目