高二下期数学巩固练习(2) 姓名
三、解答题：（共70分；要求在答卷上写出详细的计算与推演过程．）
1．正方形ABCD中，AB=2，E、F分别是边AB及BC的中点，将△AED及
△DCF折起（如图），使A、C点重合于
点．
（1）证明D⊥EF； （2）证明平面
；
（3）求D与平面DEF所成角的正切值．
 |
2. “五一”劳动节前夕，某公司召开了劳模表彰大会。来自A、B、C三个车间的6位劳模坐在公司特意放置的前排6个座位上．其中A车间1人，B车间2人，C车间3人（用数字作答）．
（1） 若每个车间的劳模派一代表介绍经验，有多少种不同的选法？
（2） 若同车间的人坐在一起，有多少种不同的坐法？
（3） 若C车间的人不坐在一起，有多少种不同的坐法？
（4） 劳模们上台领奖后仍回到前排6个座位就坐，发现只有2人坐在原位上，问有多少种不同的坐法？
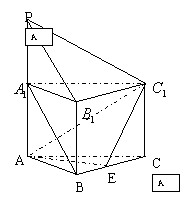3．如图，正三棱柱
的每条棱长均为2， 
， 
，E为BC中点．（1）求证：
面
；（2）求
与
所成的角；（3）求点A到面
的距离．
4．正四棱柱
的底面边长是
，侧棱长是3，点E，F分别在BB1，DD1上，且
，
．
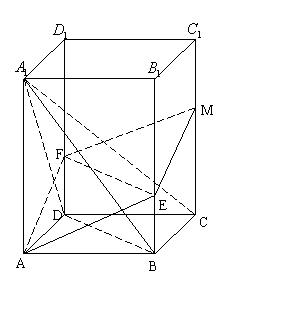①求证：
面
；②延伸平面AEF与
交于点M，求平面AEF与平面ABD所成的二面角；③求多面体ABCD-EFM的体积．
欢迎访问 http://www.k12zy.com