2007年下学期长沙市实验中学高一期中考试数学试题
高 班 姓名 记分
一、 选择题（本题共10小题，每题5分，共50分，每小题有且仅有一个答案正确）
1.已知全集U = {1 ，2 ，3 ，4 ，5 ，6 ，7 ，8 }， A= {3 ，4 ，5 }， B= {1 ，3 ，6 }，
那么集合 { 2 ，7 ，8}是 （ ）
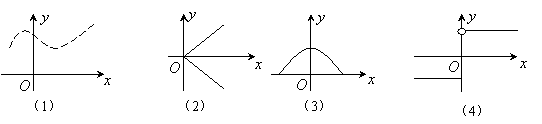2．下列四个图像中，是函数图像的是 （ ）
A、（1） B、（1）、（3）、（4） C、（1）、（2）、（3） D、（3）、（4）
3．设函数
是
上的减函数，则有 （ ）
A、
B、
C、
D、
4 . 如果集合A={xax2＋2x＋1=0}中只有一个元素，则a的值是 （ ）
(A)0 (B)0 或1 (C)1 (D)不能确定
5.已知函数
（ ）
A.3 B,2 C.1 D.0
6．下面各组函数中为相同函数的是
（ ）(A)
( B)
(C)
(D)
7．如果函数
在区间
上是减函数，那么实数
的取值范围是（ ）
A、
B、
C、
D、
8．函数y=(
)
+1+2,(x<0)的反函数为（ ）
（A）y=-
（B）
（C）y=-
（D）y=-
9．计算机成本不断降低，若每隔3年计算机价格降低1/3，现在价格为8100元的计算机，则9年后价格可降为（ ）
A. 2400元 B. 900元 Ｃ. 300元 D. 3600元
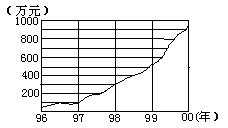10．某企业近几年的年产值如图，则年增长率最高的是（ ）（年增长率=年增长值/年产值）
A）97年 B）98年
C）99年 D）00年
二、填空题：（本大题共5小题，每小题5分，共25分，把答案填在答题卡相应位置上。）
11、 集合M={a 
∈N，且a∈Z}，用列举法表示集合M=_
12、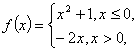
若
,则 x= .
13、化指数式
为对数式，则
.
14、函数
与函数
的图像关于
对称
15、函数
的定义域是
三、解答题:( 本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤。)
16、(本题满分12分)求值:
17.（本小题满分12分）
已知A={1，2，x2－5x＋9}，B={3，x2＋ax＋a}，如果A={1，2，3}，2 ∈B，求实数a的值.
18.（本小题满分13分）
已知M={x -2≤x≤5}, N={x a+1≤x≤2a-1}.
（Ⅰ）若M
N，求实数a的取值范围；
（Ⅱ）若M
N，求实数a的取值范围.
19、（本题满分12分）求函数
的定义域.
解:
20、（本题满分13分）已知函数
（1）判断函数的单调性,并证明;
（2）求函数和最大值和最小值.
解:
21、（本题满分13分）
如图,已知底角为450的等腰梯形ABCD,底边BC的长为7,腰长为 
,当一条平行于AB的直线L从左至右移动时,直线L把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.
解:
 |
2007年下学期长沙市实验中学高一期中考试
参 考 答 案
一、1、C；2、B; 3、D ；4、B；5、B；6、D； 7、A; 8、D; 9、C;10、 B；
二、11.｛4,3,2,-1｝,12. -3.
13．
；14.
轴；15.
三、
16、 (本题满分12分)
解:原式=
=
=
=
17. 解：由A={1，2，x2－5x＋9}＝{1，2，3}，知x2－5x＋9＝3，解得x＝2或x＝3，
又2 ∈B，则x2＋ax＋a＝2，当x＝2时，a=
，当x＝3时，a=
.
故a=或.
18. 解：（Ⅰ）由于MN，则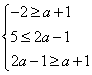
，解得a∈Φ.
（Ⅱ）①当N=Φ时，即a＋1＞2a－1，有a＜2；
②当N≠Φ，则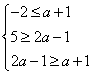
，解得2≤a≤3，
综合①②得a的取值范围为a≤3.
19、.
20、.（1）略;
（2）最大值为-2,最小值为-4.
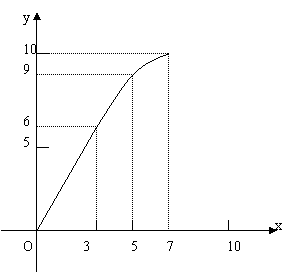21、 （1）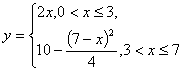
（2）图形如右