高一同步优化训练数学期中测试卷A卷（附答案）

期中测试

高中同步测控优化训练(七)

期中测试卷(A卷)

说明：本试卷分为第Ⅰ、Ⅱ卷两部分，请将第Ⅰ卷选择题的答案填入题后括号内，第Ⅱ卷可在各题后直接作答.共100分，考试时间90分钟.

第Ⅰ卷(选择题　共30分)

一、选择题(本大题共10小题，每小题3分，共30分)

1.已知A={xy=x,x∈R},B={yy=x²,x∈R},则A∩B等于

A.{xx∈R}　　　　　　　　　　　　　　　　　　　　　　　　　　　B.{yy≥0}

C.{(0,0),(1,1)}　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

解析:∵集合A代表函数y=x的定义域，∴A=R;∵集合B代表函数y=x²的值域，

∴B={yy≥0}.∴A∩B={yy≥0}.

答案:B

2.方程x²-px+6=0的解集为M,方程x²+6x-q=0的解集为N,且M∩N={2},那么p+q等于

A.21　　　　　　　　　　　　　　　　　 B.8　　　　　　　　　　　　　　　C.6　　　　　　　　　　　　　　　D.7

解析:由题意可知,2是方程x²-px+6=0且x²+6x-q=0的根,

所以2²-2p+6=0,2²+6×2-q=0.

解得p=5,q=16.

于是p+q=5+16=21.

答案:A

3.条件“<1”是条件“x>1”的

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

解析:<1<0x>1或x<0,所以<1x>1;但x>1<1,所以"<1"是"x>1"的必要不充分条件.

答案:B

4.函数f(x)=x²+2(a－1)x+2在区间(-∞,4］上递减,则a的取值范围是

A.［-3,+∞］　　　　　　　　　　　　　　　　　　　　　　　　　B.(-∞,-3)

C.(-∞,5］　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.［3,+∞)

解析:由-≥-4,得a≤5.

答案:C

5.对于任意x∈R,都有f(x+1)=2f(x),当0≤x≤1时，f(x)=x(1-x),则f(－1.5)的值是

A.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　D.-

解析:令x=－1.5,由f(x+1)=2f(x)得f(－1.5)=f(-0.5).

令x=-0.5,由f(x+1)=2f(x)得f(-0.5)=f(0.5).

∴f(－1.5)=f(-0.5)=f(0.5)=［0.5(1-0.5)］=.

答案:C

6.已知集合A到集合B={0，1，，}的映射f:x→,那么集合A中的元素最多有

A.3个　　　　　　　　　　　　　B.4个　　　　　　　　　　　　　C.5个　　　　　　　　　　　　　D.6个

解析:∵f是映射，∴A中的每一个元素都应在B中有象.

∵≠0，∴0在A中不存在原象.

当=1时，解得x=±2,

∴±2可作1的原象;

当=时，解得x=±3,

∴±3可作的原象;

当=时，解得x=±4,

∴±4可作的原象.

故A中的元素最多能有6个.

答案:D

7.已知函数f(x)=ax²+bx+c的图象如下图所示，则b的取值范围是

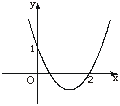
A.b>0　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.b<0

C.b<－1　　　　　　　　　　　　　　　　　　　　　　　　　　　　　D.-2<b<－1

解析:由图象得f(0)=1,即c=1.

由f(2)=0,得4a+2b+1=0.

对称轴-<2,a>0,

∴-b<4a=-2b－1b<－1.

答案:C

8.某商场对顾客实行购物优惠活动，规定一次购物付款总额：

(1)如果不超过200元，则不给予优惠；

(2)如果超过200元但不超过500元，则按标价给予9折优惠；

(3)如果超过500元，其500元内的按第(2)条给予优惠，超过500元的部分给予7折　　 优惠.

某人两次去购物，分别付款168元和423元，假设他去一次购买上述同样的商品，则应付款是

A.413.7元　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.513.7元

C.546.6元　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.548.7元

解析:购物超过200元，至少付款200×0.9=180(元)，超过500元，至少付款500×0.9=450(元)，可知此人第一次购物不超过200元，第二次购物不超过500元，则此人两次购物总额是168+=168+470=638(元).

若一次购物，应付500×0.9+138×0.7=546.6(元).

答案:C

9.若函数y=f(x)存在反函数y=f^－1(x),则下列命题中不正确的是

A.若f(x)=f^－1(x),则函数y=f(x)的图象关于y=x对称

B.函数y=f(x)的图象与直线y=x相交，则交点一定在它的反函数的图象上

C.若函数y=f(x)是(-∞,+∞)上的减函数，则其反函数y=f^－1(x)也是(-∞,+∞)上的减函数

D.函数值域中的每一个值都有原象

解析:原函数y=f(x)是(-∞,+∞)上的减函数，则其反函数y=f^－1(x)是原函数值域上的减函数.因为y=f(x)的值域未必是(-∞,+∞),故C不正确.

答案:C

10.已知f(x)=3ax+1-2a在(－1，1)上存在x₀,使得f(x₀)=0,则a的取值范围是

A.－1<a<　　　　　　　　　　　　　　　　　　　　　　　　　　B.a>

C.a>或a<－1　　　　　　　　　　　　　　　　　　　　　　　D.a<－1

解法一:f(x₀)=3ax₀+1-2a=0,显然a≠0,

∴x₀=.由题意知－1<<1,解得a>或a<－1.

解法二:当a=0时，f(x)=1,不合题意.当a≠0时，问题转化为一次函数f(x)=3ax+1-2a的图象在(－1，1)上与x轴有交点，∴f(1)·f(－1)<0,即(a+1)(-5a+1)<0,解得a>或a<－1.

答案:C

第Ⅱ卷(非选择题　共70分)

二、填空题(本大题共4小题，每小题4分，共16分)

11.已知f(x)=x²－1(x<0)，则f^－1(3)=_______.

解析:设f^－1(3)=x,则f(x)=3,即x²－1=3.

∴x=±2.∵x<0,∴x=-2.∴f^－1(3)=-2.

答案:-2

12.函数f(x)=+的定义域是_________.

解析:要使函数有意义,只需

所以,这个函数的定义域是{xx≥－1,x≠3}.

答案：{xx≥－1,x≠3}

13.某工厂8年来某产品产量y与时间t年的函数关系如下图，则：

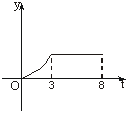
①前3年总产量增长速度增长速度越来越快；

②前3年中总产量增长速度越来越慢；

③第3年后，这种产品停止生产；

④第3年后，这种产品年产量保持不变.

以上说法中正确的是_______.

解析:由图分析，前3年总产量增长速度越来越快(曲线是下凸型)，3年后，已不再生产.

答案:①③

14.定义在R上的函数f(x)满足关系式：f(+x)+f(-x)=2,则f()+f()+…+f()的值为_______.

解析:分别令x=0,,,,

由f(+x)+f(-x)=2,

得f()+f()=2,f()+f()=2,f()+f()=2,f()+f()=2,

∴f()+f()+…+f()=7.

答案:7

三、解答题(本大题共5小题，共54分.解答应写出文字说明、证明过程或演算步骤)

15.(本小题满分10分)某热水贮存器的容量是200升,每分钟放水34升,供应热水的锅炉每t分钟注入贮存器2t²升热水.问贮存器的最小贮存量是多少?如果每人洗浴时用水65升,而贮存器水量达到最小值时放水自动停止,那么这个贮存器一次最多可供几人洗浴?

分析:贮存器内的水量由进水量与原有水量的和减去放水量而得到,求二次函数的最值可用配方法.

解:设贮存器内水量为y升,则由题设有

y=2t²-34t+200=2(t-)²+.

所以当t=8.5时,贮存器内水量y达到最小值,

此时放水停止.

总共实际放水为8.5×34=289(升).

又289÷65=4,所以一次最多可供4人洗浴.

16.(本小题满分10分)求函数y=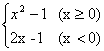的反函数.

解:当x≥0时，y≥－1,

由y=x²－1,得x=(y≥－1),

故y=x²－1(x≥0)的反函数是y=(x≥－1);

当x<0时，y<－1,

由y=2x^－1得x=(y+1)(y<－1),

故y=2x－1(x<0)的反函数是y=(x+1)(x<－1).

∴f^－1(x)=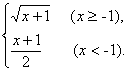

17.(本小题满分10分)已知函数f(x)=x²-4ax+2a+30,

(1)求对一切实数x,f(x)的值均为非负实数的充要条件；

(2)在(1)的条件下，求方程=a^－1+1的根的取值范围.

解:(1)依题意，f(x)≥0恒成立的充要条件是

Δ=(-4a)²-4(2a+30)=16a²-8a－120≤0，解得-≤a≤3即为所求.

(2)依题意得x=(a+3)(a－1+1)=

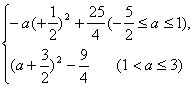
当-≤a≤1时，≤x≤;当1<a≤3时，4<x≤18.综合得≤x≤18.

18.(本小题满分12分)某家电企业根据市场调查分析，决定调整产品生产方案，准备每周(按120个工时计算)生产空调、彩电、冰箱共360台，且冰箱至少生产60台.已知生产这些家电产品每台所需工时和每台产值如下表：

家电名称	空调	彩电	冰箱
每台所需工时
每台产值(千元)	4	3	2

问每周应生产空调、彩电、冰箱各多少台，才能使周产值最高？最高产值是多少?(以千元为单位)

解:设每周生产空调、彩电、冰箱分别为x台、y台、z台，每周产值为f千元，

① ② ③

则f=4x+3y+2z，

其中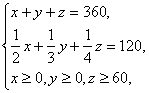

由①②可得y=360-3x,z=2x,

代入③得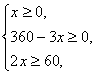则有30≤x≤120.

故f=4x+3(360-3x)+2·2x=1080-x,

当x=30时，f_max=1080-30=1050.

此时y=360-3x=270,z=2x=60.

答:每周应生产空调30台，彩电270台，冰箱60台，才能使每周产值最高，最高产值为1050千元.

19.(本小题满分12分)已知函数f(x)=(4-3a)x²-2x+a,其中a∈R,求f(x)在［0，1］上的最　　大值.

解:(1)当4-3a=0,即a=时，f(x)=-2x+为减函数.所以，f(x)在［0，1］上的最大值为f(0)= .

(2)当4-3a≠0，

即a≠时，f(x)=(4-3a)(x-)²+a-,

此时函数图象的顶点坐标为(,a-).

①当a>时，4-3a<0,f(x)的图象为开口向下的抛物线，且在［0，1］上递减，

∴［f(x)］_max=f(0)=a;

②当a≤时,0<≤,f(x)的图象开口向上且顶点横坐标在(0，)内,

∴［f(x)］_max=f(1)=2-2a;

③当<a≤1时,< ≤1,f(x)的图象开口向上且顶点横坐标在(，1］内，

∴［f(x)］_max=f(0)=a;

④当1<a<时，>1,f(x)的图象开口向上，且f(x)在［0，1］上递减，

∴［f(x)］_max=f(0)=a.