高中同步测控优化训练(八)
期中测试卷(B卷)
说明:本试卷分为第Ⅰ、Ⅱ卷两部分,请将第Ⅰ卷选择题的答案填入题后括号内,第Ⅱ卷可在各题后直接作答.共100分,考试时间90分钟.
第Ⅰ卷(选择题 共30分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.已知集合M![]() {4,7,8},且M中至多有一个偶数,则这样的集合共有
{4,7,8},且M中至多有一个偶数,则这样的集合共有
A.3个 B.4个 C.6个 D.5个
解析:集合M可以为{4,7},{7,8},{4},{7},{8},![]() 共6个.
共6个.
答案:C
2.已知a、b∈R,则"a>b"是"![]() <
<![]() "的
"的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
解析:![]() -
-![]() =
=![]() <0与a>b互不能推出.
<0与a>b互不能推出.
答案:D
3.下列四个函数中,在(0,+∞)上为增函数的是
A.f(x)=3-x B.f(x)=x2-3x
C.f(x)=-![]() D.f(x)=-x
D.f(x)=-x
答案:C
4.下列四个函数中,与y=x表示同一函数的是
A.y=(![]() )2 B.y=
)2 B.y=![]() C.y=
C.y=![]() D.y=
D.y=![]()
解析:对于A,y=(![]() )2=x(x≥0);
)2=x(x≥0);
对于B,y=![]() =x(x∈R);
=x(x∈R);
对于C,y=![]() =x=
=x=![]()
对于D,y=![]() =x(x≠0).
=x(x≠0).
答案:B
5.设全集I=R,M={xf(x)<0},N={xg(x)>0},且![]()
![]() M
M![]() N
N![]() R,则集合E={xf(x)≥0,且g(x)≤0}等于
R,则集合E={xf(x)≥0,且g(x)≤0}等于
A.![]() IM B.
IM B.![]() IN C.
IN C.
![]() D.(
D.(![]() IM)∪(
IM)∪(![]() IN)
IN)
解析:E={xf(x)≥0,且g(x)≤0}={xx∈![]() IM,且x∈
IM,且x∈![]() IN}=(
IN}=(![]() IM)∩(
IM)∩(![]() IN)=
IN)= ![]() I(M∪N)=
I(M∪N)= ![]() IN.
IN.
答案:B
6.函数y=![]() 的值域为
的值域为
A.R B.{yy≠1}
C.{yy≠0} D.{yy≠1且y≠![]() }
}
解析:y=![]() =
=![]() =1-
=1-![]() (x≠-1),所以值域为{yy≠1且y≠
(x≠-1),所以值域为{yy≠1且y≠![]() }.
}.
答案:D
7.函数y=![]() +1(x≥1)的反函数是
+1(x≥1)的反函数是
A.y=x2-2x+2(x<1)
B.y=x2-2x+2(x≥1)
C.y=x2-2x(x<1)
D.y=x2-2x(x≥1)
解析:∵y=![]() +1(x≥1),∴y≥1.
+1(x≥1),∴y≥1.
又∵y=![]() +1,∴
+1,∴![]() =y-1,
=y-1,
x-1=(y-1)2,即x=y2-2y+2.
∴所求反函数为y=x2-2x+2(x≥1).
答案:B
8.已知条件甲:![]() >0,条件乙:x-2>0,则甲是乙的
>0,条件乙:x-2>0,则甲是乙的
A.充分但不必要条件
B.必要但不充分条件
C.充要条件
D.既不充分也不必要条件
解析:甲:![]() >0
>0![]() x-3>0
x-3>0![]() x>3.
x>3.
乙:x-2>0![]() x>2.
x>2.
显然甲![]() 乙,但乙
乙,但乙![]() 甲,所以甲是乙的充分但不必要条件.
甲,所以甲是乙的充分但不必要条件.
答案:A
9.定义在(-∞,+∞)上的函数y=f(x)在(-∞,2)上是增函数,且函数y=f(x+2)图象的对称轴是x=0,则
A.f(-1)<f(3) B.f(0)>f(3)
C.f(-1)=f(-3) D.f(2)<f(3)
解析:∵y=f(x+2)关于x=0对称,∴y=f(x)关于x=2对称.
∴f(3)=f(1).
又y=f(x)在(-∞,2)上是增函数,∴f(-1)<f(1)=f(3).
答案:A
10.定义在R上的函数f(x)=-x-x3,设x1+x2≤0,给出下列不等式,其中正确不等式的序号是
①f(x1)f(-x1)≤0 ②f(x2)f(-x2)>0 ③f(x1)+f(x2)≤f(-x1)+f(-x2) ④f(x1)+f(x2)≥ f(-x1)+f(-x2)
A.①③ B.①④ C.②③ D.②④
解析:f(x)f(-x)=(-x-x3)(x+x3)=-(x+x3)2≤0,所以①正确,②不正确.易知f(x)是R上的减函数,由x1+x2≤0,知x1≤-x2,x2≤-x1,
∴f(x1)≥f(-x2),f(x2)≥f(-x1).∴f(x1)+f(x2)≥f(-x1)+f(-x2),故④正确.
答案:B
第Ⅱ卷(非选择题 共70分)
二、填空题(本大题共4小题,每小题4分,共16分)
11.满足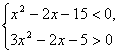 的整数x的值是_______.
的整数x的值是_______.
解析:由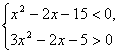 得
得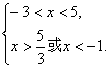
∴-3<x<-1或![]() <x<5.
<x<5.
又∵x∈Z,∴x=-2,2,3,4.
答案:-2,2,3,4
12.函数y=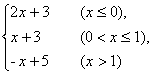 的最大值是_______.
的最大值是_______.
解析:当x≤0时,ymax=3;当0<x≤1时,ymax=4;当x>1时,-x+5<4无最大值.故y的最大值为4.
答案:4
13.若函数f(x)的图象关于原点对称,且f(x)在(0,+∞)上是增函数,f(-3)=0,则不等式xf(x)<0的解集为_______.
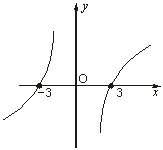
解析:由xf(x)<0得![]() 或
或![]() 由上图进而得0<x<3或-3<x<0.
由上图进而得0<x<3或-3<x<0.
答案:(-3,0)∪(0,3)
14.设函数f(x)的反函数为h(x),函数g(x)的反函数为h(x+1),已知f(2)=5,f(5)=-2,f(-2)=8,那么g(2)、g(5)、g(8)、g(-2)中,一定能求出具体数值的是_______.
解析:由h(x)=f-1(x),h(x+1)=g-1(x),
∴g-1(x)=f-1(x+1)=y,
即x=g(y),x+1=f(y).
∴g(x)=f(x)-1.
∴g(2)=f(2)-1=4,g(5)=-3,g(-2)=7.
答案:g(2),g(5),g(-2)
三、解答题(本大题共5小题,共54分.解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分10分)作出下列函数的图象,并根据图象指出函数的值域.
(1)y=![]() ;
;
(2)y=x-x-1.
解:(1)y= 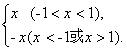
图象如下图.根据图象可知函数的值域为{y∈Ry≠1且y≠-1}.
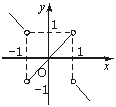
(2)y= 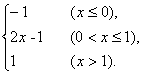
图象如下图.根据图象可知函数的值域为[-1,1].
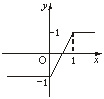
16.(本小题满分10分)设P:函数y=ax2-2x+1在[1,+∞)内单调递减,Q:曲线y=x2-2ax+
如果P与Q有且只有一个正确,求a的取值范围.
解:由P知,a=0或![]() 解得a≤0.由Q知Δ=(-
解得a≤0.由Q知Δ=(-
若P正确,Q不正确,则有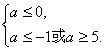 ∴a≤-1.
∴a≤-1.
若P不正确,Q正确,则有![]() ∴0<a<5.
∴0<a<5.
综上可知,a的取值范围为a≤-1或0<a<5.
17.(本小题满分12分)已知函数y=![]() (x∈[0,
(x∈[0,![]() ]),
]),
(1)求它的反函数f-1(x);
(2)判断y=f-1(x)在其定义域上的单调性并证明.
解:(1)由y=![]() 得x=±
得x=±![]() .
.
∵x∈[0,![]() ],
],
∴x=![]() .
.
∴f-1(x)=![]() ,x∈[0,5].
,x∈[0,5].
(2)y=f-1(x)在其定义域[0,5]上是减函数.
证明:设0≤x1<x2≤5.
则f-1(x1)-f-1(x2)=![]() (
(![]() -
-![]() )=
)=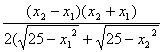 .
.
又∵0≤x1<x2≤5,∴x2-x1>0,x1+x2>0,
2(![]() +
+![]() )>0.∴f-1(x1)>f-1(x2).∴y=f-1(x)在其定义域上是减函数.
)>0.∴f-1(x1)>f-1(x2).∴y=f-1(x)在其定义域上是减函数.
18.(本小题满分10分)已知函数f(x)对任意x、y∈R,都有f(x)+f(y)=f(x+y),且当x>0时,都有f(x)<0.
(1)求f(0);
(2)证明f(x)是R上的减函数.
(1)解:令x=y=0,则有f(0)+f(0)=f(0),∴f(0)=0.
(2)证明:设x1<x2,则x2-x1>0,f(x2)=f[x1+(x2-x1)]=f(x1)+f(x2-x1).
∵x2-x1>0,
∴f(x2-x1)<0.
∴f(x2)=f(x1)+f(x2-x1)<f(x1).∴f(x)是R上的减函数.
19.(本小题满分12分)
某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元.销售单价与日均销售量的关系如下表所示:
| 销售单价/元 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 日均销售量/桶 | 480 | 440 | 400 | 360 | 320 | 280 | 240 |
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?
解:根据上表,销售单价每增加1元,日均销售量就减少40桶.设在进价基础上增加x元后,日均销售利润为y元,而在此情况下的日均销售量为
480-40(x-1)=520-40x.
由于x>0,且520-40x>0,即0<x<13,
于是可得
y=(520-40x)x-200
=-40x2+520x-200,0<x<13.
易知,当x=-![]() =6.5时,y有最大值.
=6.5时,y有最大值.
所以,只需将销售单价定为11.5元,就可获得最大的利润.