第二章 函数(一)
一、函数
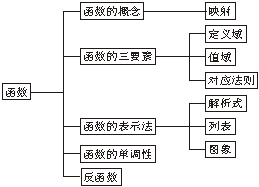
●知识网络
●范题精讲
一、函数的概念及表示
【例1】
已知f(x)=4x2-2x+1,g(x)=![]() ,求f(
,求f(![]() ),f(-x),g(
),f(-x),g(![]() ),f[g(x)],g[f(x)].
),f[g(x)],g[f(x)].
解:f(![]() )=4(
)=4(![]() )2-2·
)2-2·![]() +1=7,
+1=7,
f(-x)=4·(-x)2-2(-x)+1=4x2+2x+1,
g(![]() )=
)=![]() =
=![]() ,
,
f[g(x)]=4[g(x)]2-2[g(x)]+1
=4·(![]() )2-2·
)2-2·![]() +1
+1
=![]() ,
,
g[f(x)]=![]() =
=![]()
=![]() .
.
评注:本题是已知f、g这两个对应法则,求它们的一些函数值或由它们构造的复合函数(值).这类问题只要将自变量x或其代数式直接代入即可解决.若已知的是由两个函数复合而成的复合函数以及其中一个函数,那么怎样去求另一个函数呢?常见的方法有:待定系数法、拼凑法、换元法及消去法等.
二、函数的定义域、值域及单调性
【例2】 (1)已知f(x)的定义域为[1,2),求函数f(x2)的定义域;
(2)已知f(x+1)的定义域为[0,1],求函数f(x)的定义域.
解:(1)由f(x)的定义域为[1,2),
可知f(x2)中自变量x2也应在[1,2)中,
故1≤x2<2,∴-![]() <x≤-1或1≤x<
<x≤-1或1≤x<![]() ,
,
即f(x2)的定义域为(-![]() ,-1]∪[1,
,-1]∪[1, ![]() ).
).
(2)已知f(x)的定义域为[0,1],即0≤x≤1,
则1≤x+1≤2,∴f(x)的定义域为[1,2].
点评:该类问题关键在于正确理解函数概念,要理解定义域为自变量x的取值集合.一般地,已知f(x)的定义域为D,求f[g(x)]的定义域时,令g(x)∈D,解得x的取值范围即为f[g(x)]的定义域;已知f[g(x)]的定义域为D,求f(x)的定义域时,可由x的取值范围求得g(x)的值域,即为f(x)的定义域.
【例3】
设函数f(x)= ![]() -ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
-ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
解:任取x1、x2∈[0,+∞)且x1<x2,则
f(x1)-f(x2)=![]() -
-![]() -a(x1-x2)
-a(x1-x2)
=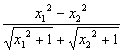 -a(x1-x2)
-a(x1-x2)
=(x1-x2)(![]() -a).
-a).
(1)当a≥1时,∵![]() <1,
<1,
又∵x1-x2<0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴a≥1时,函数f(x)在区间[0,+∞)上为减函数.
(2)当0<a<1时,在区间[0,+∞)上存在x1=0,x2=![]() ,满足f(x1)=f(x2)=1,
,满足f(x1)=f(x2)=1,
∴0<a<1时,f(x)在[0,+∞)上不是单调函数.
评注: ①判断单调性常规思路为定义法;②变形过程中![]() <1利用了
<1利用了![]() >x1≥x1,
>x1≥x1, ![]() >x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
>x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
三、反函数的理解及应用
【例4】
设函数f(x)=![]() ,已知函数y=g(x)的图象与y=f--1(x+1)的图象关于直线y=x对称,求g(3)的值.
,已知函数y=g(x)的图象与y=f--1(x+1)的图象关于直线y=x对称,求g(3)的值.
分析一:f(x)→f-1(x)→f-1(x+1)→g(x)→g(3).
解法一:由y=f(x)= ![]() ,得f--1(x)=
,得f--1(x)=
![]() ,
,
∴f--1(x+1)= ![]() .
.
又∵y=g(x)与y=f--1(x+1)的图象关于直线y=x对称,
∴y=g(x)=f--1[f--1(x+1)]=![]() .
.
∴g(3)= ![]() =
=![]() .
.
分析二:因为f--1(x+1)与f(x)和g(x)均有联系,所以借助f--1(x+1)直接找到g(x)与f(x)的关系.
解法二:由y=f--1(x+1),得x+1=f(y),
∴x=f(y)-1.
∴y=f--1(x+1)的反函数为y=g(x)=f(x)-1.
∴g(3)=f(3)-1=![]() -1=
-1=![]() .
.
分析三:利用f(a)=b![]() f--1(b)=a.
f--1(b)=a.
解法三:设g(3)=t,则g-1(t)=3,
∵g-1(x)=f--1(x+1),
∴f--1(t+1)=3.∴f(3)=t+1,t=f(3)-1=![]() -1=
-1=![]() ,即g(3)=
,即g(3)= ![]() .
.
评注:在求解与反函数有关的问题时,要充分利用原函数与反函数性质、图象间的关系.本题中注意不要将y=f--1(x+1)的反函数误认为y=f(x+1).
四、二次函数、分段函数的应用
【例5】
如图,已知底角为45°的等腰梯形ABCD,底边BC长为![]() cm
cm
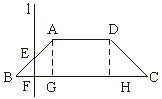
分析:要注意动直线在移动的过程中所围成的几何体的形状及相应图形的面积公式.
解:过点A、D分别作AG⊥BC,DH⊥BC,垂足分别是G、H.
因为ABCD是等腰梯形,底角为45°,AB=![]() cm
cm
所以BG=AG=DH=HC=
又BC=
(1)当点F在BG上,即x∈(0,2]时,y=![]() x2;
x2;
(2)当点F在GH上,即x∈(2,5]时,y=2+(x-2)·2=2x-2;
(3)当点F在HC上,即x∈(5,7]时,
y=S五边形ABFED=S梯形ABCD-SRt△CEF=-![]() (x-7)2+10.
(x-7)2+10.
所以,函数解析式为y=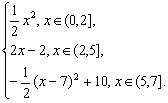
图象如图.
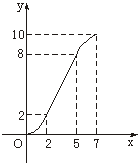
评注:在函数定义域内,对自变量x的不同取值范围有着不同的对应法则,这样的函数叫做分段函数.它的图象可以是直线、射线、线段、折线、连续的曲线、离散的点等.要不断尝试用数学表达式去表达实际问题.
●试题详解
高中同步测控优化训练(五)
第二章 函数(一)(A卷)
说明:本试卷分为第Ⅰ、Ⅱ卷两部分,请将第Ⅰ卷选择题的答案填入题后括号内,第Ⅱ卷可在各题后直接作答.共100分,考试时间90分钟.
第Ⅰ卷(选择题 共30分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.已知集合A=B=R,x∈A,y∈B,f:x→y=ax+b,若4和10的原象分别对应6和9,则19在f作用下的象为
A.18 B![]() D.28
D.28
解析:由题意![]()
![]() a=2,b=-8,
a=2,b=-8,
∴对应法则为y=2x-8.
故19在f作用下的象是y=2×19-8=30.
答案:B
2.若函数y=f(x)的定义域是[-2,4],则函数g(x)=f(x)+f(-x)的定义域是
A.[-4,4] B.[-2,2] C.[-4,-2] D.[2,4]
解析:要使函数有意义,只需![]()
![]()
![]()
![]() -2≤x≤2,
-2≤x≤2,
即函数的定义域是[-2,2].
答案:B
3.如下图可作为y=f(x)的图象的是
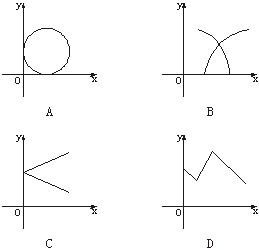
解析:在A、B、C中,均存在一个x对应两个y的情况,因此A、B、C均错.
答案:D
4.下列各组函数中,表示同一函数的是
A.f(x)=1,g(x)=x0
B.f(x)=x+2,g(x)=![]()
C.f(x)=x,g(x)=![]()
D.f(x)=x,g(x)=(![]() )2
)2
解析:判断两函数是否为同一函数,要抓住定义域和对应法则两个方面.只有定义域和对应法则完全相同的两个函数才是同一函数.
A.g(x)的定义域为x≠0,f(x)的定义域为R.
B.g(x)的定义域为x≠2,而f(x)的定义域为R.
D.g(x)的定义域为x≥0,f(x)的定义域为R.
答案:C
5.从
A.3~4万元 B.4~5万元 C.5~6万元 D.2~3万元
解析:设存款人的本金为x,根据题意可得x×2%×20%=138.64.
解得x≈3.4万元.
答案:A
6.函数y=x2+2x(x<-1)的反函数是
A.y=![]() -1(x<-1) B.y=
-1(x<-1) B.y=![]() -1(x>-1)
-1(x>-1)
C.y=-![]() -1(x<-1) D.y=-
-1(x<-1) D.y=-![]() -1(x>-1)
-1(x>-1)
解法一:x<-1时, ![]() 无意义,排除A、C.y=
无意义,排除A、C.y=![]() -1≥-1与原函数中x<-1不符,排除B,故选D.
-1≥-1与原函数中x<-1不符,排除B,故选D.
解法二:由y=x2+2x=(x+1)2-1,x<-1,得y>-1.
令y=x2+2x解得x=-1±![]() .
.
∵x<-1,∴x=-1-![]() ,
,
即y=-1-![]() (x>-1).
(x>-1).
答案:D
7.某厂日产手套总成本y(元)与手套日产量x(双)的关系式为y=5x+4000,而手套出厂价格为每双10元,则该厂为了不亏本,日产手套至少为
A.200双 B.400双 C.600双 D.800双
解析:要使该厂不亏本,只需10x-y≥0,即10x-(5x+4000)≥0,解得x≥800.
答案:D
8.已知函数f(n)=![]() 其中n∈N,则f(8)等于
其中n∈N,则f(8)等于
A.2 B
解析:f(8)=f[f(8+5)]=f[f(13)]=f(10)=7.
答案:D
9.已知映射f:A→B,其中A=B=R,对应法则f:y=-x2+2x,对于实数k∈B,在集合A中不存在原象,则k的取值范围是
A.k>1 B.k≥
解析:由题意可知,k不在函数y=-x2+2x的值域之中,由y=-x2+2x=-(x-1)2+1≤1,可得k>1.
答案:A
10.设二次函数f(x)=ax2+bx+c(a≠0),若f(x1)=f(x2)(x1≠x2),则f(x1+x2)等于
A.-![]() B.-
B.- ![]() C.c D.
C.c D. ![]()
解析:由f(x1)=f(x2) ![]() x1+x2=-
x1+x2=-![]() ,代入表达式得f(x1+x2)=f(-
,代入表达式得f(x1+x2)=f(-![]() )=
)=![]() -
-![]() +c=c.
+c=c.
答案:C
第Ⅱ卷(非选择题 共70分)
二、填空题(本大题共4小题,每小题4分,共16分)
11.函数y=![]() 的定义域为_______,值域为_______.
的定义域为_______,值域为_______.
解析:y=![]() ,故定义域为R,值域为[
,故定义域为R,值域为[![]() ,+∞).
,+∞).
答案:R [![]() ,+∞)
,+∞)
12.若函数y=ax与y=-![]() 在(0,+∞)上都是减函数,则函数y=ax2+bx在(0,+∞)上是单调递_______函数.
在(0,+∞)上都是减函数,则函数y=ax2+bx在(0,+∞)上是单调递_______函数.
解析:由已知得a<0,b<0,∴-![]() <0.
<0.
∵y=ax2+bx在[-![]() ,+∞)上单调递减,
,+∞)上单调递减,
∴y=ax2+bx在(0,+∞)上是单调递减函数.
答案:减
13.f(x)=![]() 若f(x)=10,则x=_________.
若f(x)=10,则x=_________.
解析:因为当x>0时,f(x)=-2x<0,
所以x2+1=10,解得x=±3.
又因为x≤0,所以x=-3.
答案:-3
14.已知点(-2,y1)、(![]() ,y2)、(
,y2)、(![]() ,y3)在函数y=2x2+8x+c的图象上,则y1、y2、y3从小到大依次为_______.
,y3)在函数y=2x2+8x+c的图象上,则y1、y2、y3从小到大依次为_______.
解析:∵y=2x2+8x+c在[-2,+∞)上是增函数,-2<![]() <
<![]() ,
,
∴y1<y3<y2.
答案:y1<y3<y2
评注:本题也可先求出y1、y2、y3,再比较大小.
三、解答题(本大题共5小题,共54分.解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分8分)设当x≥0时,f(x)=2;当x<0时,f(x)=1.又g(x)=![]() (x>0),写出y=g(x)的表达式,并画出其图象.
(x>0),写出y=g(x)的表达式,并画出其图象.
分析:令x-1=0,x-2=0,得x=1或2.过两个分界点把x>0分成三部分,先求出每一部分的解析式,再得出分段函数的解析式.
解:当0<x<1时,x-1<0,x-2<0,
∴g(x)=![]() =1.
=1.
当1≤x<2时,x-1≥0,x-2<0,
∴g(x)=![]() =
=![]() .
.
当x≥2时,x-1>0,x-2≥0,
∴g(x)= ![]() =2.
=2.
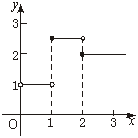
故y=g(x)=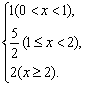
其图象如上图.
16.(本小题满分10分)求函数y=![]() 在区间[2,6]上的最大值和最小值.
在区间[2,6]上的最大值和最小值.
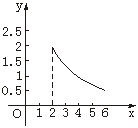
分析:由函数y=![]() (x∈[2,6])的图象(如上图)
(x∈[2,6])的图象(如上图)
可知,函数y=![]() 在区间[2,6]上递减.
在区间[2,6]上递减.
所以,函数y=![]() 在区间[2,6]的两个端点上分别取得最大值和最小值.
在区间[2,6]的两个端点上分别取得最大值和最小值.
解:设x1、x2是区间[2,6]上的任意两个实数,且x1<x2,则
f(x1)-f(x2)= ![]() -
-![]()
=![]()
=![]() .
.
由2<x1<x2<6,得x2-x1>0,(x1-1)(x2-1)>0,
于是f(x1)-f(x2)>0,即f(x1)>f(x2).
所以函数y=![]() 是区间[2,6]上的减函数.
是区间[2,6]上的减函数.
因此,函数y=![]() 在区间的两个端点上分别取得最大值与最小值,即当x=2时,ymax=2;当x=6时,ymin=
在区间的两个端点上分别取得最大值与最小值,即当x=2时,ymax=2;当x=6时,ymin=![]() .
.
17.(本小题满分12分)已知函数f(x)=![]() (x≠-a,a≠
(x≠-a,a≠![]() ).
).
(1)求f(x)的反函数;
(2)若这两个函数的图象关于y=x对称,求a的值.
解:(1)设y=![]() ,则y(x+a)=3x+1,
,则y(x+a)=3x+1,
整理得(y-3)x=1-ay.
若y=3,则a=![]() ,与已知矛盾,
,与已知矛盾,
∴x=![]() .
.
故所求反函数为f-1(x)= ![]() (x≠3).
(x≠3).
(2)依题意得f--1(x)=f(x),则![]() =
=![]() ,
,
整理得3x2-8x-3=-ax2+(1-a2)x+a,
比较两边对应项的系数,有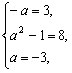
故a=-3.
18.(本小题满分12分)讨论函数f(x)=![]() 在x∈(-1,1)上的单调性.
在x∈(-1,1)上的单调性.
解:设-1<x1<x2<1,则
f(x1)-f(x2)=![]() -
-![]() =
=![]() .
.
∵x1x2+1>0,x2-x1>0,x12-1<0,x22-1<0,
∴当a>0时,f(x1)-f(x2)>0,即f(x1)>f(x2),f(x)为减函数;
当a<0时,f(x1)-f(x2)<0,即f(x1)<f(x2),f(x)为增函数;
当a=0时,f(x1)-f(x2)=0,即f(x1)=f(x2),f(x)为常函数.
19.(本小题满分12分)某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出;当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
解:(1)当每辆车月租金为3600元时,未租出的车辆数为![]() =12,所以这时租出了88辆.
=12,所以这时租出了88辆.
(2)设每辆车的月租金定为x元,则公司月收益为
f(x)=(100-![]() )(x-150)-
)(x-150)- ![]() ×50,
×50,
整理得f(x)=-![]() +162x-2100
+162x-2100
=-![]() (x-4050)2+307050,
(x-4050)2+307050,
∴当x=4050时,f(x)最大,最大值为307050 元.