高一数学指数与对数函数练习

变式练习四

　

　一、选择题

　　1．函数f（x）＝的定义域是（　　）

　　　　　 A．（1，＋∞）　　　　　　　　　　　　　　　　 B．（2，＋∞）

　　　　　 C．（－∞，2）　　　　　　　　　　　　　　　　 D．

　　解析：要保证真数大于0，还要保证偶次根式下的式子大于等于0，

　　所以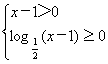解得1＜x≤2．

　　答案：D

　　2．函数y＝（x²－3x＋2）的单调递减区间是（　　）

　　　　　 A．（－∞，1）　　　　　　　　　　　　　　　　 B．（2，＋∞）

　　　　　 C．（－∞，）　　　　　　　　　　　　　　　 D．（，＋∞）

　　解析：先求函数定义域为（－o，1）∪（2，＋∞），令t（x）＝x²＋3x＋2，函数t（x）在（－∞，1）上单调递减，在（2，＋∞）上单调递增，根据复合函数同增异减的原则，函数y＝（x²－3x＋2）在（2，＋∞）上单调递减．

　　答案：B

　　3．若2（x－2y）＝x＋y，则的值为（　　）

　　　　　 A．4　　　　　　　　　　　　　　　　　　　　　　　　 B．1或

　　　　　 C．1或4　　　　　　　　　　　　　　　　　　　　　D．

　　错解：由2（x－2y）＝x＋y，得（x－2y）²＝xy，解得x＝4y或x＝y，则有＝或＝1．

　　答案：选B

　　正解：上述解法忽略了真数大于0这个条件，即x－2y＞0，所以x＞2y．所以x＝y舍掉．只有x＝4y．

　　答案：D

　　4．若定义在区间（－1，0）内的函数f（x）＝（x＋1）满足f（x）＞0，则a的取值范围为（　　）

　　　　　 A．（0，）　　　　　　　　　　　　　　　　　　B．（0，）

　　　　　 C．（，＋∞）　　　　　　　　　　　　　　　 D．（0，＋∞）

　　解析：因为x∈（－1，0），所以x＋1∈（0，1）．当f（x）＞0时，根据图象只有0＜2a＜l，解得0＜a＜（根据本节思维过程中第四条提到的性质）．

　　答案：A

　　5．函数y＝（－1）的图象关于（　　）

　　　　　 A．y轴对称　　　　　　　　　　　　　　　　　　 B．x轴对称

　　　　　 C．原点对称　　　　　　　　　　　　　　　　　　D．直线y＝x对称

　　解析：y＝（－1）＝，所以为奇函数．形如y＝或y＝的函数都为奇函数．

　　答案：C

　　二、填空题

　　已知y＝（2－ax）在［0，1］上是x的减函数，则a的取值范围是__________．

　　解析：a＞0且a≠1（x）＝2－ax是减函数，要使y＝（2－ax）是减函数，则a＞1，又2－ax＞0a＜（0＜x＜1）a＜2，所以a∈（1，2）．

　　答案：a∈（1，2）

　　7．函数f（x）的图象与g（x）＝（）^x的图象关于直线y＝x对称，则f（2x－x2）的单调递减区间为______．

　　解析：因为f（x）与g（x）互为反函数，所以f（x）＝x

　　则f（2x－x²）＝（2x－x²），令（x）＝2x－x²＞0，解得0＜x＜2．

　　（x）＝2x－x²在（0，1）上单调递增，则f［（x）］在（0，1）上单调递减；

　　（x）＝2x－x²在（1，2）上单调递减，则f［（x）］在［1，2）上单调递增．

　　所以f（2x－x²）的单调递减区间为（0，1）．

　　答案：（0，1）

　　8．已知定义域为R的偶函数f（x）在［0，＋∞］上是增函数，且f（）＝0，

　　则不等式f（log₄x）的解集是______．

　　解析：因为f（x）是偶函数，所以f（－）＝f（）＝0．又f（x）在［0，＋∞］上是增函数，所以f（x）在（－∞，0）上是减函数．所以f（log₄x）＞0log₄x＞或log4x＜－．

　　解得x＞2或0＜x＜．

　　答案：x＞2或0＜x＜

　　三、解答题

　　9．求函数y＝（x²－5x＋4）的定义域、值域和单调区间．

　　解：由（x）＝x2－5x＋4＞0，解得x＞4或x＜1，所以x∈（－∞，1）∪（4，＋∞），当x∈（－∞，1）∪（4，＋∞），｛｜＝x²－5x＋4｝＝R^＋，所以函数的值域是R^＋．因为函数y＝（x²－5x＋4）是由y＝（x）与（x）＝x²－5x＋4复合而成，函数y＝（x）在其定义域上是单调递减的，函数（x）＝x²－5x＋4在（－∞，）上为减函数，在［，＋∞］上为增函数．考虑到函数的定义域及复合函数单调性，y＝（x²－5x＋4）的增区间是定义域内使y＝（x）为减函数、（x）＝x²－5x＋4也为减函数的区间，即（－∞，1）；y＝（x²－5x＋4）的减区间是定义域内使y＝（x）为减函数、（x）＝x²－5x＋4为增函数的区间，即（4，＋∞）．

　　10．设函数f（x）＝＋，

　　（1）求函数f（x）的定义域；

　　（2）判断函数f（x）的单调性，并给出证明；

　　（3）已知函数f（x）的反函数f^－1（x），问函数y＝f^－1（x）的图象与x轴有交点吗?若有，求出交点坐标；若无交点，说明理由．

　　解：（1）由3x＋5≠0且＞0，解得x≠－且－＜x＜．取交集得－＜x＜．

　　（2）令（x）＝3x＋5，随着x增大，函数值减小，所以在定义域内是减函数；

　　＝－1＋随着x增大，函数值减小，所以在定义域内是减函数．

　　又y＝lgx在定义域内是增函数，根据复合单调性可知，y＝是减函数，所以f（x）＝＋是减函数．

　　（3）因为直接求f（x）的反函数非常复杂且不易求出，于是利用函数与其反函数之间定义域与值域的关系求解．

　　设函数f（x）的反函数f^－1（x）与工轴的交点为（x₀，0）．根据函数与反函数之间定义域与值域的关系可知，f（x）与y轴的交点是（0，x₀），将（0，x₀）代入f（x），解得x₀＝．所以函数y＝f^－1（x）的图象与x轴有交点，交点为（，0）。

欢迎访问 http://www.k12zy.com