成都市2006~2007学年度上期期末调研考试高二数学
一、选择题:每小题5分共60分
1、两个平面有公共点,则公共点的个数是( )
A、1个 B、2个 C、无数个 D、一个或无数个
2、在空间任取四点,它们可以确定的平面个数只能是( )
A、1个 B、2个或3个 C、4个 D、一个或4个或无数个
3、若抛物线的顶点在坐标原点,对称轴为x轴,焦点在直线2x-4y+11=0上,则它的方程为( )
A、![]() B、
B、 ![]() C、
C、![]() D、
D、![]()
4、中心在坐标原点,准线方程为x=![]() 4,离心率为
4,离心率为![]() 的椭圆方程为( )
的椭圆方程为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、经过点A(1,2),并且在两个坐标轴上的截距的绝对值相等的直线共有( )
A、1条 B、2条 C、3条 D、4条
6、已知向量![]() 与向量
与向量![]() 平行,则实数k为( )
平行,则实数k为( )
A、![]() B、-
B、-![]() C、
C、![]() D、-
D、-![]()
7、有如下命题:①若直线![]() ;
;
②若直线![]() ;
;
③若直线![]() ;
;
④若直线![]() 。其中正确命题是( )
。其中正确命题是( )
A、①、④ B、①、③ C、② D、均不正确
8、在空间,下列结论正确的是( )
A、过一点,有且仅有一条直线与已知直线垂直
B、过平面外一点,有且只有一个平面与已知平面平行
C、过平面外一点,有且只有一条直线与已知平面平行
D、过直线外一点,有且只有一个平面与已知直线平行
9、设PQ是过双曲线焦点F1且垂直于实轴的弦,F2是双曲线的另一个焦点,若![]() ,则此双曲线的离心率e=( )
,则此双曲线的离心率e=( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
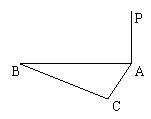 10、在
10、在![]() 中,AB=AC=5,BC=6,
中,AB=AC=5,BC=6,![]() ,PA=8,则点P到BC的距离是( )
,PA=8,则点P到BC的距离是( )
A、![]() B、2
B、2![]() C、3
C、3![]() D、4
D、4![]()
11、当曲线![]() 与直线
与直线![]() 有两个交点时,实数k的取值范围是( )
有两个交点时,实数k的取值范围是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、若椭圆![]() 内有一点P(1,-1),F是其右焦点,椭圆上一点M,使得|MP|+2|MF|值最小,则点M的坐标为( )
内有一点P(1,-1),F是其右焦点,椭圆上一点M,使得|MP|+2|MF|值最小,则点M的坐标为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
二、填空题:每小题5分共20分
 13、已知:
13、已知:![]() ,
,![]() ,
,![]() ,
,![]() 的坐标为_________________________________
的坐标为_________________________________
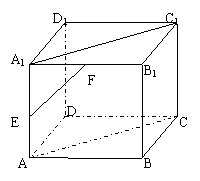
14、如图,正方体ABCD-A1B1C1D1中,E、F分别是AA1、A1B1的中点,则EF与平面A1C1CA所成的角的度数是__________________
 15、已知x、y满足约束条件
15、已知x、y满足约束条件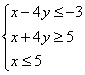 ,则目标函数
,则目标函数![]() 的最大值为________________________
的最大值为________________________
16、在右边的坐标系中,画出方程![]() 所表示曲线的草图。
所表示曲线的草图。
三、解答题:
17、(共8分)求与已知直线![]() 关于点(1,-1)对称的直线
关于点(1,-1)对称的直线![]() 的方程。
的方程。
18、(共11分)一个圆经过点P(2,-1),且与直线![]() 相切,圆心在直线
相切,圆心在直线![]() 上,求该圆的方程。
上,求该圆的方程。
19、(共12分)
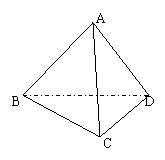
(文科做)已知:如图,在空间四边形ABCD中,![]()
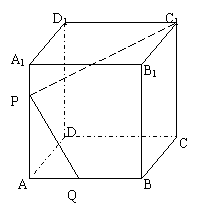
 (理科做)如图,已知棱长为a的正方体ABCD-A1B1C1D1中,P是棱AA1上的一点,且
(理科做)如图,已知棱长为a的正方体ABCD-A1B1C1D1中,P是棱AA1上的一点,且![]() 。
。
(I)度在AB上找出一点Q,使C1P![]() PQ;
PQ;
(II)求当C1P![]() PQ时,线段AQ的长。
PQ时,线段AQ的长。
20、(共12分)
(文科做):已知双曲线过点A(-2,4)和B(4,4),它的一个焦点是抛物线![]() 的焦点,求它的另一个焦点的轨迹方程。
的焦点,求它的另一个焦点的轨迹方程。
(理科做):已知:如图,![]() 的边BC长为16,AC、AB边上中线长的和为30。
的边BC长为16,AC、AB边上中线长的和为30。
求:(I)![]() 的重心G的轨迹;(II)顶点A的轨迹方程。
的重心G的轨迹;(II)顶点A的轨迹方程。
21、(共14分)
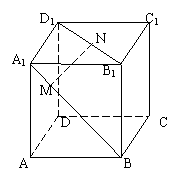 已知:如图,在单位正方体ABCD-A1B1C1D1中,M是A1B上的点,
已知:如图,在单位正方体ABCD-A1B1C1D1中,M是A1B上的点,![]() ,N是B1D1上的点,
,N是B1D1上的点,![]() 。
。
求证:(I)MN是异面直线A1B与B1D1的公垂线;
(II)求线段MN的长。
22、(共13分)
(文科做):已知顶点在坐标原点,焦点在x轴上的抛物线被直线![]() 截得的弦长为
截得的弦长为![]() ,求此抛物线方程。
,求此抛物线方程。
(理科做:)已知A(1,1)是椭圆![]() 上一点,F1、F2是椭圆的两个焦点,且满足|AF1|+|AF2|=4。
上一点,F1、F2是椭圆的两个焦点,且满足|AF1|+|AF2|=4。
(I)求两焦点的坐标;
(II)设点C、D是椭圆上的两点,直线AC、AD的倾斜角互补,直线CD的斜率是否为定值?若是定值,求出其值;若不是定值,则说明理由。
欢迎访问 http://www.k12zy.com