高中同步测控优化训练(六)
第二章 函数(一)(B卷)
说明:本试卷分为第Ⅰ、Ⅱ卷两部分,请将第Ⅰ卷选择题的答案填入题后括号内,第Ⅱ卷可在各题后直接作答.共100分,考试时间90分钟.
第Ⅰ卷(选择题 共30分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列各式中,表示y是x的函数的有
①y=x-(x-3);②y=![]() +
+![]() ;③y=
;③y=![]() ④y=
④y=![]()
A.4个 B.3个 C.2个 D.1个
解析:①③表示y是x的函数;在②中由![]() 知x∈
知x∈![]() ,因为函数定义域不能是空集,所以②不表示y是x的函数;在④中若x=0,则对应的y的值不唯一,所以④不表示y是x的函数.
,因为函数定义域不能是空集,所以②不表示y是x的函数;在④中若x=0,则对应的y的值不唯一,所以④不表示y是x的函数.
答案:C
2.函数f(x)=2x2-mx+3,当x∈[-2,+∞)时是增函数,当x∈(-∞,-2]时是减函数,则f(1)等于
A.-3 B
解析:由题意可知,x=-2是f(x)=2x2-mx+3的对称轴,即-![]() =-2,
=-2,
∴m=-8.∴f(x)=2x2+8x+3.
∴f(1)=13.
答案:B
3.已知f(x)=3x+1(x∈R),若f(x)-4<a的充分条件是x-1<b(a、b>0),则a、b之间的关系为
A.a≤![]() B.b≤
B.b≤![]() C.b>
C.b>![]() D.a>
D.a>![]()
解析:f(x)-4<a等价于x-1<![]() ,
,
由x-1<b![]() x-1<
x-1<![]() ,
,
∴b≤![]() .
.
答案:B
4.函数f(x)=![]() (a、b、c是常数)的反函数是f--1(x)=
(a、b、c是常数)的反函数是f--1(x)=![]() ,则a、b、c的值依次是
,则a、b、c的值依次是
A.2,1,3 B.-2,-1,
解析:由f-1(x)=
![]() 解得f(x)=
解得f(x)= ![]() =
=![]() .
.
又f(x)=
![]() ,∴a=-2,b=-1,c=-3.
,∴a=-2,b=-1,c=-3.
答案:B
5.已知函数f(x)=![]() 的定义域是一切实数,则m的取值范围是
的定义域是一切实数,则m的取值范围是
A.0<m≤4 B.0≤m≤
解析:要使函数有意义,只需对任意x∈R,不等式mx2+mx+1≥0恒成立.
当m=0时,1≥0,显然成立.
当m≠0时,只需![]()
![]()
![]()
![]() 0<m≤4.
0<m≤4.
综上可知,0≤m≤4.
答案:D
6.设f(x)>0是定义在区间I上的减函数,则下列函数中增函数的个数是y=3![]() y=[f(x)]2 y=1-
y=[f(x)]2 y=1-![]()
A.1
B
解析:因为f(x)>0且f(x)在I上是减函数,故y=3![]() ,y=1-
,y=1-![]() 为I上的增函数,故选C.
为I上的增函数,故选C.
答案:C
7.对于任意x1、x2∈[a,b],满足条件f(![]() )>
)>![]() [f(x1)+f(x2)]的函数f(x)的图象是
[f(x1)+f(x2)]的函数f(x)的图象是
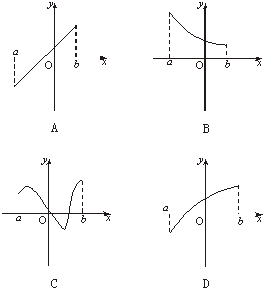
解析:对于A有f(x)为一次函数,显然f(![]() )=
)=![]() [f(x1)+f(x2)].
[f(x1)+f(x2)].
对于D如下图所示,任取x1<x2,则
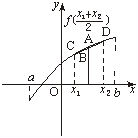
f(![]() )的值为对应点A的纵坐标,
)的值为对应点A的纵坐标,![]() [f(x1)+f(x2)]的值为对应线段CD中点B的纵坐标,显然A在B上方,故选D.
[f(x1)+f(x2)]的值为对应线段CD中点B的纵坐标,显然A在B上方,故选D.
答案:D
8.函数f(x)=x+![]() 的图象是
的图象是
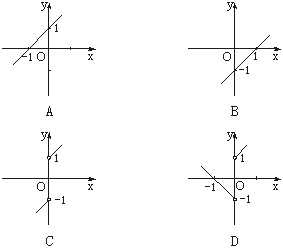
解析:f(x)=![]()
答案:C
9.已知函数y=f(x)(x∈[a,b]),那么集合{(x,y)y=f(x),x∈[a,b]}∩{(x,y)x=2}中所含元素的个数为
A.1
B
解析:此题即求y=f(x)(x∈[a,b])与直线x=2的交点个数,不注意对应法则常误选A,其原因在于未注意2是否属于[a,b].若2∈[a,b],则交点为1个;若2![]() [a,b],则交点为0个.
[a,b],则交点为0个.
答案:C
10.定义在R上的函数y=f(x-1)是单调递减函数(如下图所示),给出四个结论,其中正确结论的个数是
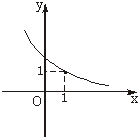
①f(0)=1 ②f(1)<1 ③f-1(1)=0
④f--1(![]() )>0
)>0
A.1 B
解析:由图知,当x=1时,f(x-1)=1,即f(0)=1.
∴①正确.
∵y=f(x)的反函数存在,
∴f--1(1)=0.
∴③正确.
由题意知x=2时,f(x-1)<1,即f(1)<1.
∴②正确.
∵y=f(x-1)单调递减,
∴y=f--1(x)单调递减.
由图知, ![]() <f(0),
<f(0),
∴f--1(![]() )>f--1[f(0)]=0.
)>f--1[f(0)]=0.
∴④正确.
答案:D
第Ⅱ卷(非选择题 共70分)
二、填空题(本大题共4小题,每小题4分,共16分)
11.已知函数f(x)= ![]() ,则f(1)+f(2)+…+f(2002)+f(2003)+f(1)+f(
,则f(1)+f(2)+…+f(2002)+f(2003)+f(1)+f(![]() )+…+f(
)+…+f(![]() )+f(
)+f(![]() )=_______.
)=_______.
解析:∵f(x)+f(![]() )=
)=![]() +
+![]() =1,
=1,
∴原式=2003×1=2003.
答案:2003
12.如果f[f(x)]=2x-1,则一次函数f(x)=_________.
解析:用待定系数法求函数解析式.
设f(x)=ax+b(a≠0),则
f[f(x)]=af(x)+b=a(ax+b)+b
=a2x+ab+b.
由f[f(x)]=2x-1,得![]()
解得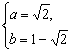 或
或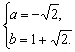
所以f(x)=![]() x+1-
x+1-![]() ,或f(x)=-
,或f(x)=- ![]() x+1+
x+1+![]() .
.
答案: ![]() x+1-
x+1-![]() 或-
或-![]() x+1+
x+1+![]()
13.对于定义在R上的函数f(x),若实数x0满足f(x0)=x0,则称x0是函数f(x)的一个不动点.若函数f(x)=x2+ax+1没有不动点,则实数a的取值范围是_______.
解析:f(x)无不动点等价于方程x2+ax+1=x无解,
即(a-1)2-4<0![]() -1<a<3.
-1<a<3.
答案:-1<a<3
14.已知f(x)是R上的增函数,A(0,-1),B(3,1)是其图象上的两个点,那么f(x+1)<1的解集是_________.
解析:f(x+1)<1即-1<f(x+1)<1,
∴f(0)<f(x+1)<f(3).
∵f(x)在R上单调递增,
∴0<x+1<3.
∴-1<x<2.
答案:{x-1<x<2}
三、解答题(本大题共5小题,共54分.解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分8分)如图,动点P从边长为4的正方形ABCD顶点B开始,顺次经过C、D、A绕周界一圈,设x表示P的行程,y表示△APB的面积,求函数y=f(x)的解析式.
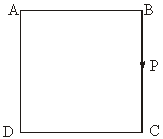
解:设PB=x,∵AB=4,由三角形面积公式,得
y=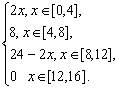
16.(本小题满分10分)若二次函数f(x)=ax2+bx+c(a≠0)的图象关于y轴对称,且f(-2)>f(3),设m>-n>0,试比较f(m)和f(n)的大小,并说明理由.
解:∵f(x)=ax2+bx+c(a≠0)的图象关于y轴对称,
∴对任意x∈R,恒有f(-x)=f(x),
即a(-x)2+b(-x)+c=ax2+bx+c恒成立.
∴2bx=0对任意x∈R恒成立.
∴b=0.∴f(x)=ax2+c.
∵f(-2)>f(3),且f(-2)=f(2),
∴f(2)>f(3).∴a<0.
∴f(x)在(0,+∞)上是减函数.
又∵m>-n>0,
∴f(m)<f(-n).
而f(-n)=f(n),
∴f(m)<f(n).
17.(本小题满分12分)设a∈R,函数f(x)=x2+x-a+1,x∈R,求f(x)的最小值.
解:(1)当x≥a时,f(x)=x2+x-a+1
=(x+![]() )2-a+
)2-a+![]() ,
,
若a≤-![]() 时,则f(x)在[a,+∞)上的最小值为f(-
时,则f(x)在[a,+∞)上的最小值为f(-![]() )=
)=![]() -a;
-a;
若a>-![]() 时,则f(x)在[a,+∞)上单调递增,
时,则f(x)在[a,+∞)上单调递增,
f(x)min=f(a)=a2+1.
(2)当x≤a时,f(x)=x2-x+a+1=(x-![]() )2+a+
)2+a+![]() ];
];
若a≤![]() 时,则f(x)在(-∞,a]上单调递减,f(x)min=f(a)=a2+1;
时,则f(x)在(-∞,a]上单调递减,f(x)min=f(a)=a2+1;
当a>![]() 时,则f(x)在(-∞,a]上的最小值为f(
时,则f(x)在(-∞,a]上的最小值为f(![]() )=
)=![]() +a.
+a.
综上所述,当a≤-![]() 时,f(x)的最小值为
时,f(x)的最小值为![]() -a;
-a;
当-![]() <a≤
<a≤![]() 时,f(x)的最小值为a2+1;
时,f(x)的最小值为a2+1;
当a>![]() 时,f(x)的最小值为
时,f(x)的最小值为![]() +a.
+a.
18.(本小题满分12分)有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是P和Q(万元),它们与投入资金x(万元)的关系有经验公式:P=![]() x,Q=
x,Q=![]()
![]() .今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少,能获得的最大利润为多少?
.今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少,能获得的最大利润为多少?
解:设对甲种商品投资x万元,获总利润为y万元,则对乙种商品的投资为(3-x)万元,于是y=![]() x+
x+![]()
![]() (0≤x≤3).
(0≤x≤3).
令t=![]() (0≤t≤
(0≤t≤![]() ),则x=3-t2,
),则x=3-t2,
∴y=![]() (3-t2)+
(3-t2)+ ![]() t=
t=![]() (3+3t-t2)
(3+3t-t2)
=-![]() (t-
(t-![]() )2+
)2+![]() ,t∈[0,
,t∈[0,![]() ].
].
∴当t=![]() 时,ymax=
时,ymax=![]() =1.05(万元);
=1.05(万元);
由t=![]() 可求得x=0.75(万元),
可求得x=0.75(万元),
3-x=2.25(万元),
∴为了获得最大利润,对甲、乙两种商品的资金投入应分别为0.75万元和2.25万元,获得最高利润1.05万元.
19.(本小题满分12分)济南市某电脑公司在市区和微山湖各有一分公司,市区分公司现有电脑6台,微山湖分公司有同一型号的电脑12台.淄博某单位向该公司购买该型号电脑10台,济南某单位向该公司购买该型号电脑8台,已知市区运往淄博和济南每台电脑的运费分别是40元和30元,微山湖运往淄博和济南每台电脑的运费分别是80元和50元.
(1)设从微山湖调运x台至淄博,该公司运往淄博和济南的总运费为y元,求y关于x的函数关系式.
(2)若总运费不超过1000元,问能有几种调运方案?
(3)求总运费最低的调运方案及最低运费.
解:(1)若微山湖调运x台至淄博,则运(12-x)台至济南,市区运(10-x)台至淄博,运往济南6-(10-x)=(x-4)台(4≤x≤10,x∈N),
则y=80x+50(12-x)+40(10-x)+30(x-4)
=20x+880,
所以y=20x+880(x∈N,且4≤x≤10).
(2)由y≤1000,得20x+880≤1000,解得x≤6.
又因为x∈N,且4≤x≤6,所以x=4、5、6,
即有3种调运方案.
(3)因为y为增函数,所以当x=4时,ymin=960.
故从微山湖运4台至淄博,运8台至济南,市区运6台至淄博,运费最低.