第二章 函数(二)
二、指数函数与对数函数
●知识网络
●范题精讲
一、指数及对数运算
【例1】 (1)已知
=3,求
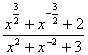的值；
(2)已知lg(x+y)+lg(2x+3y)－lg3=lg4+lgx+lgy,求
的值.
(1)分析:由分数指数幂运算性质可求得
和x2+x－2的值.
解:∵=3，
∴
=33－3×3=18.
x2+x－2=(x+x－1)2－2=［(
－2］2－2=(32－2)2－2=47.
∴原式=
.
(2)分析:注意x、y的取值范围，去掉对数符号，找到x、y的关系式.
解:由题意可得x>0,y>0,由对数运算法则得
lg(x+y)(2x+3y)=lg(12xy),
则(x+y)(2x+3y)=12xy.
(2x－y)(x－3y)=0,
即2x=y或x=3y.
故
或=3.
评注:条件代数式的求值问题包括以下三个方面:(1)若条件简单,结论复杂,可从化简结论入手用上条件;(2)若条件复杂,结论简单,可从化简条件入手,转化成结论的形式;(3)若条件与结论的复杂程度相差无几时,可同时对它们进行化简,直到找出它们之间的联系为止.
对于齐次方程的化简,也可在方程两边同除以某一齐次项,把方程转化成要求的代数式为未知数的方程的形式.
二、指数函数、对数函数的性质应用
【例2】
已知函数y=
(a2x)·loga2(
)(2≤x≤4)的最大值为0，最小值为－
，求a的值.
解:y= (a2x)·loga2()
=－loga(a2x)［－
loga(ax)］
=(2+logax)(1+logax)
=(logax+
)2－,
∵2≤x≤4且－≤y≤0,∴logax+=0,即x=
时，ymin=－.
∵x≥2>1,∴>1
0<a<1.
又∵y的最大值为0时，logax+2=0或logax+1=0,
即x=
或x=
.∴=4或=2.
又∵0<a<1,∴a=.
评注:(1)若不注意发现隐含条件"0<a<1"则会造成不必要的分类讨论.
(2)在最值问题中以二次函数为内容的最值最常见，而且许多表面上非二次函数最值问题通过适当变形都可以转化为二次函数最值.
三、指数函数、对数函数图象的应用
【例3】 已知a＞0，且a≠1，函数y=ax与y=loga(－x)的图象只能是下图中的
解法一:首先，曲线y=ax只可能在上半平面，y=loga(－x)只可能在左半平面上，从而排除A、C.
其次，从单调性着眼,y=ax与y=loga(－x)的增减性正好相反，又可排除D.
∴应选B.
解法二:若0＜a＜1，则曲线y=ax下降且过点(0,1)，而曲线y=loga(－x)上升且过(－1，0),以上图象均不符合这些条件.
若a＞1，则曲线y=ax上升且过点(0，1)，而曲线y=loga(－x)下降且过(－1，0)，只有B满足条件.
解法三:如果注意到y=loga(－x)的图象关于y轴的对称图象为y=logax，又y=logax与y=ax互为反函数(图象关于直线y=x对称)，则可直接选定B.
评注:要养成从多角度分析问题，解决问题的习惯，培养思维的灵活性.
四、函数应用举例
【例4】
某企业实行裁员增效，已知现有员工a人，每人每年可创纯利润1万元，据评估在生产条件不变的条件下，每裁员一人，则留岗员工每人每年可多创收0.01万元，但每年需付给下岗工人0.4万元生活费，并且企业正常运行所需人数不得少于现有员工的
，设该企业裁员x人后纯收益为y万元.
(1)写出y关于x的函数关系式，并指出x的取值范围;
(2)当140<a≤280时，问该企业应裁员多少人，才能获得最大的经济效益.(注：在保证能获得最大经济效益的情况下，能少裁员，应尽量少裁)
解:(1)由题意可得
y=(a－x)(1+0.01x)－0.4x=－
x2+(
－
)x+a.
∵a－x≥ax≤
,
即x的取值范围是(0, ]中的自然数.
(2)∵y=－［x－(
－70)］2+ (－70)2+a
且140<a≤280,∴－70∈(0,].
∴当a为偶数时，x=－70,y取最大值;
当a为奇数时，x=
－70或x=
－70.
∵尽可能少裁人，∴x=－70.
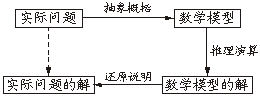
评注:应用题的解题过程:
●试题详解
高中同步测控优化训练(九)
第二章 函数(二)(A卷)
说明：本试卷分为第Ⅰ、Ⅱ卷两部分，共100分，考试时间90分钟.
第Ⅰ卷(选择题 共30分)
一、选择题(本大题共10小题，每小题3分，共30分)
1.已知集合A={yy=log2x,x＞1},B={yy=()x,x＞1},则A∩B等于
A.{y0＜y＜}
B.{y0＜y＜1}
C.{y＜y＜1}
D. 
解析:∵y=log2x,x＞1,∴y＞0,即A={yy＞0}.
又∵y=()x,x＞1,∴0＜y＜,即B={y0＜y＜＝.
∴A∩B={yy＞0}∩{y0＜y＜}={y0＜y＜}.
答案:A
2.函数y=
(x2－6x+17)的值域是
A.R B.［8，+∞)
C.(－∞,－3) D.［－3,+∞)
解析:y=［(x－3)2+8］≤8=－3.
答案:C
3.下列结论中正确的个数是
①当a＜0时，
=a3 ②
=a ③函数y=
－(3x－7)0的定义域是(2, +∞) ④若
A.0 B
解析:取a=－2，可验证①不正确；
当n为奇数时，②不正确；
③y=－(3x－7)0的定义域应是［2，
］∪(，+∞);
④由100a=5,得102a=5. (1) 又10b=2, (2)
(1)×(2)得102a+b=10.
∴2a+b=1,此命题正确.
答案:B
4.函数y=
的定义域是
A.(1，2］
B.(1，2)
C.(2，+∞)
D.(－∞,2)
解析:由题意得
1＜x＜2.
答案:B
5.设有两个命题:①关于x的不等式x2+2ax+4>0对于一切x∈R恒成立，
②函数f(x)=－(5－2a)x是减函数，若此二命题有且只有一个为真命题，则实数a的范围是
A.(－2,2) B.(－∞,2)
C.(－∞,－2) D.(－∞,－2]
解析:①等价于Δ=(2a)2－16<0－2<a<2.
②等价于5－2a>1a<2.
①②有且只有一个为真，
∴a∈(－∞,－2).
答案:C
6.二次函数y=ax2+bx与指数函数y=(
)x的图象只可能是
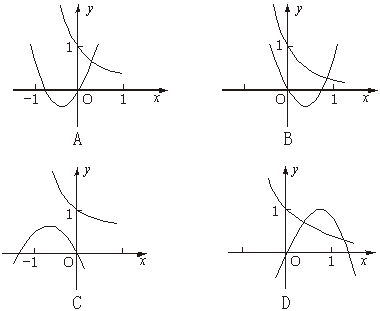
解析:由y=()x的图象知0＜＜1,
∴－＜－
＜0,即二次函数y=ax2+bx的对称轴在－到0之间.
答案:A
7.已知函数y=f(x)的反函数为f－1(x)=2x+1,则f(1)等于
A.0 B.1 C.－1 D.4
解析:令f(1)=x,则f－1(x)=1,令2x+1=1,
∴x=－1.
答案:C
8.若定义在区间(－1，0)内的函数f(x)=log2a(x+1)满足f(x)>0,则a的取值范围是
A.(0,) B.(0,
]
C.( ,+∞) D.(0,+∞)
解析:f(x)=log2a(x+1)>0=log2a1.
∵x∈(－1,0),∴0＜x+1<1.
∴0<2a<1,即0<a<.
答案:A
9.右图是指数函数①y=ax,②y=bx,③y=cx,④y=dx的图象,则a、b、c、d与1的大小关系是
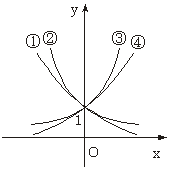
A.a＜b＜1＜c＜d B.b＜a＜1＜d＜c
C.1＜a＜b＜c＜d D.a＜b＜1＜d＜c
解析:因为任何底数的一次幂都是底数本身,所以,可作直线x=1,它同各个图象相交,交点的纵坐标就是各指数函数的底数.
答案:B
10.设lg2=a,lg3=b,则log512等于
A.
B.
C.
D.
解析:log512=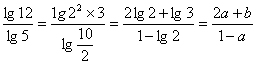
.
答案:C
第Ⅱ卷(非选择题 共70分)
二、填空题(本大题共4小题，每小题4分，共16分)
11.方程
=3的解是_________.
解析:由=3得3·32x+2·3x－1=0.
∴3x=
或3x=－1(舍).
∴x=－1.
答案:－1
12.1992年底世界人口达到54.8亿,若人口的年平均增长率为1%,经过x年后世界人口数为 y亿,则y与x的函数解析式为_________.
解析:1992年底世界人口为54.8亿.
1年后的人口数为
y1=54.8+54.8×1%=54.8×(1+1%);
2年后的人口数为
y2=54.8×(1+1%)+54.8×(1+1%)×1%=54.8×(1+1%)2;
3年后的人口数为
y3=54.8×(1+1%)3;
……
x年后的人口数为y=54.8×(1+1%)x.
答案:y=54.8×(1+1%)x
13.若不等式3x2－2ax>()x+1对一切实数x恒成立，则实数a的取值范围为_______.
解析:由题意知x2－2ax>－x－1恒成立,
即x2－(2a－1)x+1>0恒成立.
故Δ=(2a－1)2－4<0－
.
答案:－
14.关于x的方程7x+1－7x·a－a－5=0有负根，则a的取值范围是_________.
解法一:由7x+1－7x·a－a－5=0得a=
=7－
，
∵x＜0，∴1＜7x+1＜2.
∴6＜＜12.
∴－5＜a＜1.
解法二:由7x+1－7x·a－a－5=0得7x=
.
∵x＜0,∴0＜7x＜1.∴0＜＜1.
解得－5＜a＜1.
答案:－5＜a＜1
三、解答题(本大题共5小题，共54分.解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分8分)
一种放射性元素,最初的质量为500 g,按每年10%衰减.
(1)求t年后,这种放射性元素质量ω的表达式;
(2)由求出的函数表达式,求这种放射性元素的半衰期(剩留量为原来的一半所需的时间叫做半衰期).(精确到0.1.已知lg2=0.3010,lg3=0.4771)
解:(1)最初的质量为500 g.
经过1年后,ω=500(1－10%)=500×0.91;
经过2年后,ω=500×0.9(1－10%)=500×0.92;
由此推知,t年后,ω=500×0.9t.
(2)解方程500×0.9t=250,
0.9t=0.5,
lg0.9t=lg0.5,
tlg0.9=lg0.5,
t=
≈6.6(年),
即这种放射性元素的半衰期约为6.6年.
16.(本小题满分10分)甲、乙两人解关于x的方程:log2x+b+clogx2=0,甲写错了常数b，得到根
、；乙写错了常数c，得到根、64.求这个方程真正的根.
解:原方程可变形为log22x+blog2x+c=0.
由于甲写错了常数b，得到的根为和，
∴c=log2·log2=6.
由于乙写错了常数c,得到的根为和64,
∴b=－(log2+log264)=－5.
故原方程为log22x－5log2x+6=0.
因式分解得(log2x－2)(log2x－3)=0.
∴log2x=2或log2x=3，即x=4或x=8.
17.(本小题满分12分)试讨论函数f(x)=loga
(a＞0且a≠1)在(1,+∞)上的单调性,并予以证明.
分析:本题考查复合函数单调性的判定方法,判定的法则是同增异减,判定的关键是分清函数的复合过程.
解:设u=,任取x2＞x1＞1,则
u2－u1=
=
=
.
∵x1＞1,x2＞1,∴x1－1＞0,x2－1＞0.
又∵x1＜x2,∴x1－x2＜0.
∴＜0,即u2＜u1.
当a＞1时,y=logax是增函数,∴logau2＜logau1,
即f(x2)＜f(x1);
当0＜a＜1时,y=logax是减函数,∴logau2＞logau1,
即f(x2)＞f(x1).
综上可知,当a＞1时,f(x)=loga在(1,+∞)上为减函数;当0＜a＜1时,f(x)=loga在(1,+∞)上为增函数.
18.(本小题满分12分)设f(x)=lg
，且当x∈(－∞,1］时f(x)有意义，求实数a的取值范围.
解:欲使x∈(－∞,1]时，f(x)有意义，需1+2x+4xa＞0恒成立，也就是a＞
－［()x+()x］(x≤1)恒成立.
∵u(x)=－［()x+()x］在(－∞,1］上是增函数，
∴当x=1时，［u(x)］max=－.
于是可知，当a＞－时，满足题意,
即a的取值范围为(－，+∞).
19.(本小题满分12分)某种细菌每隔两小时分裂一次(每一个细菌分裂成两个，分裂所需时间忽略不计)，研究开始时有两个细菌，在研究过程中不断进行分裂，细菌总数y是研究时间t的函数，记作y=f(t).
(1)写出函数y=f(t)的定义域和值域；
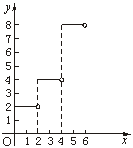
(2)在所给坐标系中画出y=f(t)(0≤t<6)的图象；
(3)写出研究进行到n小时(n≥0，n∈Z)时，细菌的总数有多少个(用关于n的式子表示).
解:(1)y=f(t)定义域为t∈［0,+∞),
值域为{yy=2n,n∈N*}.
(2)0≤t<6时，为一分段函数
y=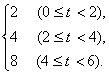
图象如下图.
(3)n为偶数时，y=
;
n为奇数时，y=
.
∴y=