2007学年奉贤区调研测试高一数学试卷
（完卷时间90分钟，满分100分） 08.1
一、填空题：(本大题满分33分。第1至第9每题3分,第10题6分)
1、已知A＝
, B＝
，则A∩B＝
。
2、方程
的解为
。
3、
＋3的值为 。
4、若f(x)＝x
，g(x)＝
，则
__________________。
5、函数
(x >0) 的反函数为
。
6、如果一个分式不等式的解集是（1,2］，这个不等式可以是_______________。
7、函数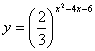
的单调递减区间是________________。
8、定义运算“＃”：a＃b
，
且
。若2＃x≥2，则实数x的取值范围是
。
9、奇函数
的定义域为R，函数
。若
，则
的值为 。
10、命题：“函数f(x)＝
在(0,＋∞)上是单调递增函数”。此命题为 （填：真或假）命题。理由：
。
二、选择题：(本大题满分15分。每题3分,)
11、如果b<a<0,那么下列不等式中错误的是（ ）
（A）c＋b <c＋a（B）
< 
（C） b
<a （D）
<
12、用反证法证明命题：“a，b∈
，ab可被5整除，那么a，b中至少有一个能被5整除”时，假设的内容应为
（ ）
（A） a，b都能被5整除 （B） a，b都不能被5整除
（C） a，b不都能被5整除 （D） a不能被5整除
13、根据表格中的数据，可以判定方程
的一个根所在的区间为 ( )
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
A. 
B. 
C. 
D. 
14、已知
，常数
，则
是
成立的…………（ ）
（A）充要条件（B）充分不必要条件（C）必要不充分条件（D）既不充分又不必要条件
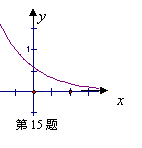15、函数
的图像如图所示，其中a、b为常数，则下列结论正确的是（ ）
(A)
(B)
(C)
(D)
三、解答题：（ 本大题共有5题，满分52分，解答下列各题必须写出必要的步骤）
16、（本题8分）
求解方程：
(x＋1)＋
(x－3)＝1
解：
17、（本题9分）
设集合A 表示函数
的值域，B表示不等式
解集。求A∩
B。
解：
18、（本题满分11分，第1小题4分，第2小题7分）
已知函数
。
(1)若函数y=
的图像过点
，求实数
的值；
(2)试讨论函数 y=的奇偶性，并说明理由.
解：
19、（本题满分11分，第1小题5分，第2小题6分）
甲、乙两商场同时促销原销售价为2000元的某种型号的彩电。甲商场一律按销售价的8折促销，即按原价的80％销售。乙商场按如下方式促销：买一台优惠2.5％，买两台优惠5％，买三台优惠7.5％，依此类推，即每多买一台，每台再优惠2.5个百分点，但每台最低价不能低于1500元。某公司需购买这种型号的彩电x台（
）。若到甲商场购买的费用为元，到乙商场购买的费用为
元。（1）分别求出函数、的关系式；（2）问去哪家商场购买花费较少？并说明理由。
解：
20、（本题满分13分，第1小题4分，第2小题4分，第3小题5分）
已知定义在区间
上的函数
具有如下性质：在区间
上单调递增，在区间
上单调递减，且
（其中
）。现给定函数
，请你根据上述知识解决下列问题：
（1）求出的定义域；
（2）对于任意的
，当
时，比较
和
的大小；
（3）若
的解集为非空集合，求整数m的最小值。
解：
2007学年奉贤区调研测试高一数学试卷参考答案
一、填空题：(本大题满分33分。第1至第9每题3分,第10题6分)
1、
2、
3、
4、
5、
6、
等
7、
或
8、
9、
10、假；反例：如
，但
，不满足单调递增函数的定义。
二、选择题：(本大题满分15分。每题3分,)
11、C 12、B 13、C 14、C 15、D
三、解答题：（ 本大题共有5题，满分52分，解答下列各题必须写出必要的步骤）
16、（本题8分）
解：
，
（3分）
，
，
。
（3分）
经检验，是原方程的解。
（2分，“经检验”遗漏扣1分）
17、（本题9分）
解：
,
（3分）
（2分）
，
（2分）
。
（2分）
18、（本题满分11分，第1小题4分，第2小题7分）
解：(1)因为函数y=
的图像过点
，
所以
，解得
；
（4分）
(2)①当
时，
，
（1分）
它的定义域为R关于原点对称，
又对任意x∈R，都有
成立，
（2分）
所以函数
为奇函数；
（1分）
②当
时,
函数的定义域为(-∞,
)∪(,+∞)不关于原点对称, （2分）
所以函数为非奇非偶函数。
（1分）
19、（本题满分11分，第1小题5分，第2小题6分）
略解：（1）到甲商场购买的费用为
， （2分）
到乙商场购买的费用为
。（3分）
（2）分段作差比较得出：
当
时，去甲商场购买花费较少； （2分）
当
时，去甲、乙商场购买花费一样；
（2分）
当
时，去乙商场购买花费较少。
（2分）
20、（本题满分13分，第1小题4分，第2小题4分，第3小题5分）
解：（1）由
可得定义域为
；
（4分）
（2）
。
（2分）
由性质可知，在区间
上是单调递增的，
因为
，且
，所以
；
（2分）
（3）
，
由性质可知，在定义域上的最小值为
， （3分）
所以
，即整数m的最小值为5。
（2分）