高一数学函数的性质的测验

　函数的性质单元测验　

新化县第十一中学  康华业

一.选择题.

1.知f(x)是实数集上的偶函数，且在区间上是增函数，则的大小关系是（　　　）

Ａ． Ｂ．Ｃ．Ｄ．

２. 定义在区间（－∞，＋∞）上的奇函数ｆ（ｘ）为增函数，偶函数ｇ（ｘ）在［０，＋∞上图象与ｆ(ｘ)的图象重合.设ａ＞ｂ＞０，给出下列不等式，其中成立的是( 　　 )　

 ①ｆ（ｂ）－ｆ（－ａ）＞ｇ（ａ）－ｇ（－ｂ）

②ｆ（ｂ）－ｆ（－ａ）＜ｇ（ａ）－ｇ（－ｂ）

③ｆ（ａ）－ｆ（－ｂ）＞ｇ（ｂ）－ｇ（－ａ）

④ｆ（ａ）－ｆ（－ｂ）＜ｇ（ｂ）－ｇ（－ａ）

Ａ.①④　　　　Ｂ.②③　　　　Ｃ.①③　　　　Ｄ.②④

３. 函数f(x)=x²-2ax-3在区间[1，2]上是单调函数的条件是　　　　　　　　　　  （  ）　

A.  B. C. D.

４. 若函数是奇函数，当x<0时，f(x)的解析式是f(x)=x(1-x),则当x>0时，f(x)的解析式是（　　 ）.

A.-x(1-x) B.x(1-x) C.-x(1+x) D.x(1+x)

５. 定义在（－１，１）上的函数ｆ（ｘ）是奇函数，并且在（－１，１）上ｆ（ｘ）是减函数，求满足条件ｆ（１－ａ）＋ｆ（１－ａ^２）＜０的ａ取值范围.　（　　　　）　

Ａ．（０，１）　Ｂ．（－２，１）　Ｃ．［０，１］　Ｄ．［－２，１］

６. 已知函数ｆ（ｘ)是定义在区间［－２，２］上的偶函数，当ｘ∈［０，２］时，ｆ(ｘ)是减函数，如果不等式ｆ（１－ｍ）＜ｆ（ｍ）成立，求实数ｍ的取值范围.（　　　）

Ａ．　　Ｂ．［１，２］　　　Ｃ．［－１，０］　Ｄ．（）

二.填空题.　

　７.若ｆ（ｘ）是偶函数，其定义域为Ｒ，且在上是减函数，则ｆ（2a²+a+1）<f(3a²-2a+1)的a的取值集合为.

8.已知f(x)是奇函数，定义域为{xxR且x0},又f(x)在（0，+）上是增函数，且f(-1)=0,则满足f(x)>0的x取值范围是.

9.若f(x)是定义在R上的偶函数，且当x0时为增函数，那么使f()<f(a)的实数a的取值范围是.

10.都是奇函数，f(x)=+2在（0，+）上有最大值5，则f(x)在（-，0）上有最值.

三.解答题 .　

11．设函数ｆ（ｘ）在（－∞，０）∪（０，＋∞）上是奇函数，又ｆ（ｘ）在（０，＋∞）上是减函数，并且ｆ（ｘ）＜０，指出Ｆ(ｘ）＝在（－∞，０）上的增减性?并证明.

12.设f(x)是定义在（0,+）上的单调递增函数，且对定义域内任意x,y,都有f(xy)=f(x)+f(y),f(2)=1,求使不等式f(x)+f(x-3)2成立的取值范围.

试题答案（供参考）

一.

1.D 2.C 3.D.　4.D 5.　A　 6. A

二.

7. （0，3）

8.(-1,0)(1,+)

9.或

10.小，-1.

三.11.证明：

F（x）在（-，0）上是增函数.证明过程如下：

设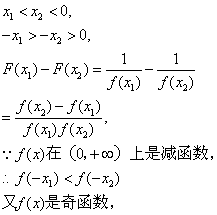

　

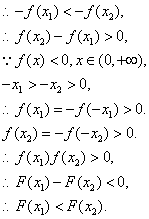
　  F（x）在（-，0）上是增函数.

12..

欢迎访问 http://www.k12zy.com