知识网络检测题(四)
(立体几何)
一、选择题
1、一个顶点上三条棱长分别为3、4、5, 且它的八个顶点都在同一个球面上，这个球表面积为（ ）
A.
B.
C.
D.
2、在下列条件中，可判断平面
与
平行的是（
）
A．、都垂直于平面
B. 内存在不共线三点到的距离相等
C.
、
是内两条直线，且∥，∥
D. 、是两条异面直线，且∥，∥，∥，∥
3、一凸多面体的棱数为30，面数为12，则它的各面多边形的内角和为（ ）
A．5400° B．6480° C．7200° D．7920°
4、在北纬60°圈上，有A、B两地，它们在纬度圈上的弧长等于
，（R为地球的半径），则这两地的球面距离是（ ）
A．
B．
C．
D．
5、已知三棱锥D—ABC的三个侧面与底面全等，且AB=AC=
，BC=2，二面角A—BC—D的平面角为（
）
A.
B.
C.
D. 
6、从正方体的6个面中选3个面，其中有2个面不相邻的选法共有（ ）
7、多面体ABC—DEFG中，AB、AC、AD两两互相垂直，
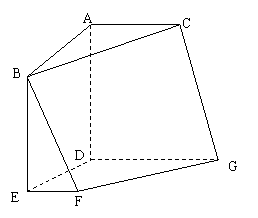平面ABC∥平面DEFG，平面BEF∥平面ADGC；
AB=AD=DG=2，AC=EF=1，
则该多面体的体积为（ ）
A．8 B．6 C．4 D．2
A.8种 B.12种 C.16种 D.20种
8、正四棱锥的侧棱与底面所成角的余弦值为x，则相邻两侧面所成二面角的余弦值f (x)等于（ ）
A．
B．
C．
D．
9、在正三棱锥P—ABC中，M、N分别是PB、PC的中点，且截面AMN⊥面PBC，则此三棱锥的侧棱和底面所面的角的正切值（ ）
A.
B.
C.
D.
10、在直三棱柱ABC—A1B1C1中AA1=AB=AC，AB⊥AC1，M是CC1的中点，Q为BC的中点，点P在A1B1上，则PQ和AM所成角为（ ）
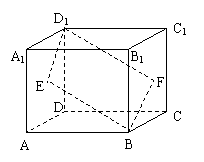A.30° B.45° C.60° D.90°
二、填空题
11、已知m，l是直线，、是平面，给出下列命题：
①若l垂直于内的两条相交直线则l⊥
②若l∥，则l平行于内所有直线
③若
，
且l⊥m，则⊥
④若
，且⊥，则⊥
⑤若，，且∥，则m∥l
其中正确的命题的序号是
12、如图：直四棱柱A1B1C1D1—ABCD中，当底面四边形ABCD满足条件 时，有A1C⊥B1D1
13、、是两不同的个平面，m、n是平面及之外两条不同的直线 .给出四个论断：
①m⊥n ②⊥
③n⊥
④m⊥
以其中三个论断为条件，余下一个论断为结论，写出你认为正确的一个命题：
14、如图：E、F分别有正方体ABCD—A1B1C1D1，面ADD1A1，面BCC1B1的中心，则四边形BFD1E在该正方体的面上的射影可能是
 |  | ||||||||||||
|
| ||||||||||||
 |  | ||||||||||||
| |||||||||||||
| |||||||||||||
三、解答题
15、四棱锥P—ABCD的底面边长为a的下方形，PB⊥平面ABCD
（1） 若面PAD与面ABCD所成二面角为60°，求这个四棱锥的体积.
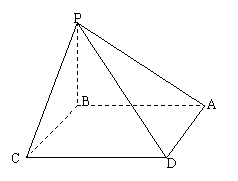（2）证明无论四棱锥的高怎样变化，面PAD与面PCD所成二面角恒大于90°.
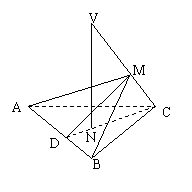
16、已知VC是△ABC所在平面的一条斜线，点N是V在平面ABC上的射影且在△ABC的高CD上.
（1） 证明：∠MDC是二面角M—AB—C的平面角.
（2） 当∠MDC=∠CVN时，证明：面ABM⊥面VNC.
 | |||
 | |||
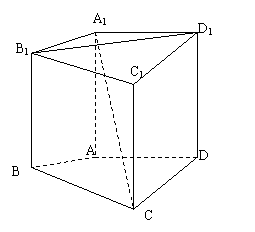
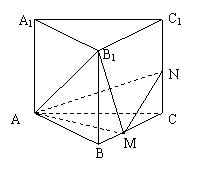17、正三棱柱ABC—A1B1C1的所有棱长都为a，M是BC的中点，N是CC1上一点且MN⊥AB1.
（1） 求证：B1M⊥MN且NC=
（2） 求点C1到面AMN的距离
 |
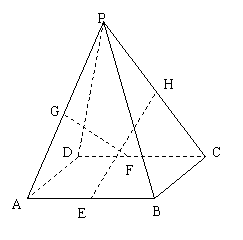
18、下四棱锥P—ABCD的各条棱长相等，E、F、G、H分别是AB、CD、PA、PC的中点.
（1） 求证：GF∥平面PBC
（2） 求异面直线GF与HE所成角的余弦值.
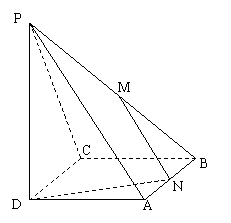
19、已知四棱锥P—ABCD的底面是边长为4的正方形，PD⊥底面ABCD，PD=6，M、N分别为PA、PB的中点.
（1） 求证：MN⊥CD.
（2） 求二面角M—DN—C的平面角的正切值.