第五章向量月考题

月考检测题（100分钟）

一、　　　　　 选择题：10×4＝40分

1.下列说法中正确的个数有（　　）

①相等的向量必共线，共线的向量必相等　　②

③　　④　　 ⑤

A.1　　 B.2　　C.3　 D.4

2.若向量，则（　　）

A.　　 B. 　　C. 　 D.

3.已知的夹角为135^O，则（　　）

A.12　　 B.3　　C.6　 D.

4.已知点A(x,5)关于点C(1，y)的对称点是B(-2,-3)，则点P(x,y)到原点的距离是（　 ）

A.4　　 B.　　C.　　 D.

5.已知P₁(-1,-6)，P₁(3,0),则点P分所成的比为λ及y的值是（　　）

A.和-8　　　　B. 和－8  　　　 C. 和4　　　D. 和-4

6.将函数的图像按平移后的函数解析式为（　　）

A.  B. 　 C. 　D.

7.在△ABC中，已知，则a=（　　）

A.　 B. 　 C.　　D.

8. 在△ABC中，若acosA=bcosB，则△ABC是（　　）

A.等腰三角形　 B.等边三角形　 C.直角三角形　D.等腰三角形或直角三角形

9. 在△ABC中，已知b=x,a=2,A=45^o，如果利用正弦定理理解三角形时有两解，则x的取值范围是（　　）

A.　 B.　 C.x>2　 D.x<2

10.在△ABC中，若三边满足a²-c²+b²=ab，则∠C=（　 ）

A.60^O  B.45^O或135^O　　　C.120^O D.30^O

二、填空题: 4×4＝16分

11.已知向量是与共线的单位向量，则_____________

12.已知为单位向量，当与之间的夹角为120^o时，在方向上的投影是______

13.已知A(2,3),B(1,4),，且，则α＋β＝__________

14.在△ABC中，A=60^o,b=10,c=4,若S_△ABC=,则此三角形内切圆的半径r＝__________

三、解答题（共44分）

15. 已知＝（4，3），＝（－1，2），＝－λ，＝2+，按照下列条件求λ的值。（12分）

（1）　　　　  （2）//，并回答是同向平行还是反方向平行　　

（3）＝　　　　 （4），的夹角为钝角

16.已知ΔABC中，三边a，b，c满足a＝4，b+c＝5，且有tanA+tanB＝tanAtanB－，求此三角形的面积。（10分）

17.已知函数y＝－2（x－2）²－1，经过按平移后使得抛物线顶点在y轴上，且在x轴截得弦长为4，求平移后得函数解析式，求。（6分）

18.已知ΔABC三个顶点A（0，8），B（－4，0），C（5，－3）点D在线段AB上，且BD＝3AD,E在BC上，若S_ΔBDE＝S_ΔABC，求E点的坐标。（6分）

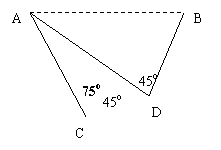
19.隔河看两目标A与B，但不能到达，在岸边选取相距千米的C，D两点，用测角仪测得BCD＝45^o，ADC＝30^o，ADB＝45^o（A、B、C、D在同一平面内）求两目标A、B之间的距离。（10分）

30o

　　　　　　　　　　　　　　　　　　　 

　高 一 数 学 月 考 答 题 纸

题号	一	二	三	总分
得分

  一、选择题：（每题4分，共40分）

题号	1	2	3	4	5	6	7	8	9	10
答案

　　　　　　　　　

　　二、填空题：（每空4分，共16分）

11．_________________。　　　　 12．_________________。 　 

13．_________________。　　　　  14．_________________。 　　　　　　　　 

　 三、解答题：(共44分)

　 15．

16．

17．

18．

19．