圆锥曲线
1.圆锥曲线的两个定义：
（1）第一定义中要重视“括号”内的限制条件：
（1）已知定点
，在满足下列条件的平面上动点P的轨迹中是椭圆的是 A．
B．
C．
D．
（答：C）；
（2）方程
表示的曲线是_____ （答：双曲线的左支）
（2）第二定义
已知点
及抛物线
上一动点P（x,y）,则y+PQ的最小值是_____
（答：2）
2.圆锥曲线的标准方程
（1）椭圆：
（1）已知方程
表示椭圆，则
的取值范围为____
（答：
）；
（2）若
，且
，则
的最大值是____，
的最小值是___（答：
）
（2）双曲线：
（1）双曲线的离心率等于
，且与椭圆
有公共焦点，则该双曲线的方程_______
（答：
）；
（2）设中心在坐标原点
，焦点
、
在坐标轴上，离心率
的双曲线C过点
，则C的方程为_______
（答：
）
（3）抛物线：
3.圆锥曲线焦点位置的判断：
椭圆：
已知方程
表示焦点在y轴上的椭圆，则m的取值范围是__
（答：
）
4.圆锥曲线的几何性质：
（1）椭圆
（1）若椭圆
的离心率
，则
的值是__ （答：3或
）；
（2）以椭圆上一点和椭圆两焦点为顶点的三角形的面积最大值为1时，则椭圆长轴的最小值为__
（答：
）
（2）双曲线
（1）双曲线的渐近线方程是
，则该双曲线的离心率等于______
（答：
或
）；
（2）双曲线
的离心率为
，则
= （答：4或
）；
（3）设双曲线
（a>0,b>0）中，离心率e∈[
,2],则两条渐近线夹角θ的取值范围是________
（答：
）；
（3）抛物线；设
，则抛物线
的焦点坐标为________（答：
）；
5、点
和椭圆
（
）的关系：
6．直线与圆锥曲线的位置关系：
（1）若直线y=kx+2与双曲线x2-y2=6的右支有两个不同的交点，则k的取值范围是_______（答：(-
,-1)）；
（2）直线y―kx―1=0与椭圆
恒有公共点，则m的取值范围是_______
（答：[1，5）∪（5，+∞））；
（3）过双曲线
的右焦点直线交双曲线于A、B两点，若│AB︱＝4，则这样的直线有_____条 （答：3）；
（2）过双曲线
＝1外一点的直线与双曲线只有一个公共点的情况如下：①P点在两条渐近线之间且不含双曲线的区域内时，有两条与渐近线平行的直线和分别与双曲线两支相切的两条切线，共四条；②P点在两条渐近线之间且包含双曲线的区域内时，有两条与渐近线平行的直线和只与双曲线一支相切的两条切线，共四条；③P在两条渐近线上但非原点，只有两条：一条是与另一渐近线平行的直线，一条是切线；④P为原点时不存在这样的直线；
（3）过抛物线外一点总有三条直线和抛物线有且只有一个公共点：两条切线和一条平行于对称轴的直线。
（1）过点
作直线与抛物线
只有一个公共点，这样的直线有______（答：2）；（2）过点(0,2)与双曲线
有且仅有一个公共点的直线的斜率的取值范围为______
（答：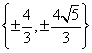
）；
（3）过双曲线
的右焦点作直线
交双曲线于A、B两点，若
4，则满足条件的直线有____条
（答：3）；
（4）对于抛物线C：
，我们称满足
的点
在抛物线的内部，若点在抛物线的内部，则直线：
与抛物线C的位置关系是_______
（答：相离）；
（5）过抛物线
的焦点
作一直线交抛物线于P、Q两点，若线段PF与FQ的长分别是
、
，则
_______（答：1）；
（6）设双曲线
的右焦点为，右准线为，设某直线交其左支、右支和右准线分别于
，则
和
的大小关系为___________(填大于、小于或等于) （答：等于）；
（7）求椭圆
上的点到直线
的最短距离（答：
）；
（8）直线
与双曲线
交于
、
两点。①当
为何值时，、分别在双曲线的两支上？②当为何值时，以AB为直径的圆过坐标原点？
（答：①
；②
）；
7、焦半径
（1）已知椭圆
上一点P到椭圆左焦点的距离为3，则点P到右准线的距离为____
（答：
）；
（2）已知抛物线方程为
，若抛物线上一点到
轴的距离等于5，则它到抛物线的焦点的距离等于____；
（3）若该抛物线上的点
到焦点的距离是4，则点的坐标为_____（答：
）；（4）点P在椭圆
上，它到左焦点的距离是它到右焦点距离的两倍，则点P的横坐标为_______（答：
）；
（5）抛物线
上的两点A、B到焦点的距离和是5，则线段AB的中点到轴的距离为______（答：2）；（6）椭圆
内有一点
，F为右焦点，在椭圆上有一点M，使
之值最小，则点M的坐标为_______（答：
）；
8、焦点三角形
（1）短轴长为
，离心率
的椭圆的两焦点为
、
，过作直线交椭圆于A、B两点，则
的周长为________（答：6）；
（2）设P是等轴双曲线
右支上一点，F1、F2是左右焦点，若
，PF1=6，则该双曲线的方程为
（答：
）；
（3）椭圆
的焦点为F1、F2，点P为椭圆上的动点，当·<0时，点P的横坐标的取值范围是 （答：
）；
（4）双曲线的虚轴长为4，离心率e＝
，F1、F2是它的左右焦点，若过F1的直线与双曲线的左支交于A、B两点，且
是
与
等差中项，则＝__________（答：
）；
（5）已知双曲线的离心率为2，F1、F2是左右焦点，P为双曲线上一点，且
，
．求该双曲线的标准方程（答：
）；
9、抛物线中与焦点弦有关的一些几何图形的性质：
10、弦长公式：
（1）过抛物线y2=4x的焦点作直线交抛物线于A（x1，y1），B（x2，y2）两点，若x1+x2=6，那么AB等于_______ （答：8）；
（2）过抛物线
焦点的直线交抛物线于A、B两点，已知AB=10，O为坐标原点，则ΔABC重心的横坐标为_______
（答：3）；
11、圆锥曲线的中点弦问题：
（1）如果椭圆
弦被点A（4，2）平分，那么这条弦所在的直线方程是 （答：
）；
（2）已知直线y=－x+1与椭圆
相交于A、B两点，且线段AB的中点在直线L：x－2y=0上，则此椭圆的离心率为_______
（答：
）；
（3）试确定m的取值范围，使得椭圆
上有不同的两点关于直线
对称
（答：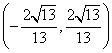
）；
特别提醒：因为
是直线与圆锥曲线相交于两点的必要条件，故在求解有关弦长、对称问题时，务必别忘了检验！
12．你了解下列结论吗？
与双曲线
有共同的渐近线，且过点
的双曲线方程为_______
（答：
）
13．动点轨迹方程：
已知动点P到定点F(1,0)和直线
的距离之和等于4，求P的轨迹方程．
（答：
或
）；
线段AB过x轴正半轴上一点M（m，0）
，端点A、B到x轴距离之积为
）；
(1)由动点P向圆
作两条切线PA、PB，切点分别为A、B，∠APB=600，则动点P的轨迹方程为 （答：
）；
（2）点M与点F(4,0)的距离比它到直线
的距离小于1，则点M的轨迹方程是_______ （答：
）；
(3) 一动圆与两圆⊙M：
和⊙N：
都外切，则动圆圆心的轨迹为 （答：双曲线的一支）；
动点P是抛物线
上任一点，定点为
,点M分
所成的比为2，则M的轨迹方程为__________（答：
）；
（1）AB是圆O的直径，且AB=
，使
，求点的轨迹。（答：
）；
（2）若点
在圆
上运动，则点
的轨迹方程是____（答：
）；
（3）过抛物线
的焦点F作直线交抛物线于A、B两点，则弦AB的中点M的轨迹方程是________（答：
）；
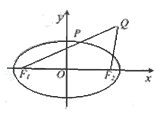已知椭圆
的左、右焦点分别是F1（－c，0）、F2（c，0），Q是椭圆外的动点，满足
点P是线段F1Q与该椭圆的交点，点T在线段F2Q上，并且满足
（1）设
为点P的横坐标，证明
；（2）求点T的轨迹C的方程；（3）试问：在点T的轨迹C上，是否存在点M，使△F1MF2的面积S=
若存在，求∠F1MF2的正切值；若不存在，请说明理由. （答：（1）略；（2）
；（3）当
时不存在；当
时存在，此时∠F1MF2＝2）