直线、平面、简单几何体

高二复习训练题

直线、平面、简单几何体

班级__________　姓名__________　学号__________　评分__________

一、选择题（本小题共12小题，每小题5分，共60分）

1．下面推理错误的是（　 ）

　　 A．，，，

　　 B．，，，直线

　　 C．，

　　 D．、、，、、且、、不共线、重合

2．在空间四边形中，、、、上分别取、、、四点，

如果、交于一点，则（　 ）

　　 A．一定在直线上　　  　　　　　　　　　B．一定在直线上

　　 C．在直线或上　　　　　　　　　　　D．既不在直线上，也不在上

3．如图S为正三角形所在平面ABC外一点，且SA＝SB＝BC＝AB，E、F分别为SC、AB中点，则异面直线EF与SA所成角为（　 ）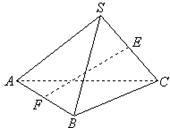

　　 A．90º　　　　　　　　　　 　　　　　　　　　　　　　　　　B．60º　　　　　　　　　　

　　 C．45º　 　　　　　　　　 　　　　　　　　　　　　　　　　D．30º

4．下列说法正确的是（　 ）

　　 A．若直线平行于平面内的无数条直线，则

　　 B．若直线在平面外，则

　　 C．若直线，，则

　　 D．若直线，，则直线就平行于平面内的无数条直线

5．在下列条件中，可判断平面与平面平行的是（　 ）

　　 A．、都垂直于平面

　　 B．内存在不共线的三点到平面的距离相等

　　 C．、是内两条直线，且，

　　 D．、是两条异面直线，且，，，

6．已知、是平面，、是直线，下列命题中不正确的是（　 ）

　　 A．若，，则　　 　　　B．若，，则

　　 C．若，，则　　　　 D．若，，则

7．把正方形ABCD沿对角线AC折起，当点D到平面ABC的距离最大时，直线BD和平面ABC所成角的大小为（　 ）

　　 A．90º　　　　　　　　　　 B．60º　　　　　　　　　　 C．45º　 　　　　　　　　 D．30º

8．PA、PB、PC是从点P引出的三条射线，每两条射线的夹角均为60º，则直线PC与平面APB所成角的余弦值是（　 ）

　　 A．　　　　　　　　　　　B．　　　　　　　　　 C．　 　　　　　　　 D．

9．正方体ABCD—A₁B₁C₁D₁中，E、F分别是AA₁、AB的中点，则EF与对角面A₁C₁CA所成角的度数是（　 ）

　　 A．30º　 　　　　　　　　 B．45º　 　　　　　　　　 C．60º　 　　　　　　　　 D．150º

10．二面角P—a—Q为60º，如果平面P内一点A到平面Q的距离为，则A在平面Q上的射影A₁到平面P的距离为（　 ）

　　　 A．1　 　　　　　　　　　B．　 　　　　　　　 C．　 　　　　　　　 D．2

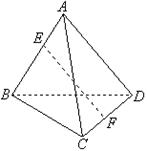11．如图，正四面体ABCD中，E在棱AB上，F在棱CD上，使得,记，其中表示EF与AC所成的角，表示EF与BD所成角，则（ 　）

　A．在单调递增　 B．在单调递减

　　 C．在单调递增，而在单调递减　　 D．在为常数

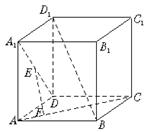
12．如图，正方体ABCD—A₁B₁C₁D₁中，EF是异面直线AC、A₁D的公垂线，则EF与BD₁的关系为（　 ）

　　　 A．相交不垂直　 　　　　　　　　　　　　　　　　　 B．相交垂直

　　　 C．异面直线　　　　　　　　　　　　　　　　　　　　D．平行直线

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二、填空题（本大题共4小题，每小题4分，共16分）

13．设是直二面角，，，，，

则　　　　  。

14．、、是两两垂直且交于O点的三个平面，P到平面、、的距离分别是2、3、

6，则　　　　  。

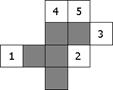
15．一个正方体的表面展开图的五个正方形如图阴影部分，第六个正方形

在编号1—5的适当位置，则所有可能的位置编号为　　　　  。

16．已知、是异面直线，那么：①必存在平面过且与平行；②必存在平面过且与垂直；③必存在平面与、都垂直；④必存在平面与、距离都相等，

其中正确的命题的序号为　　　　　。

三、解答题（本大题共6小题，共74分）

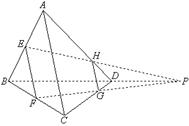17．如图，在空间四边形ABCD中，E、F分别是AB、BC的中点，G、H分别是CD、DA上的点，且，，

求证：EH、FG必相交于一点，且交点在BD的延长线上。

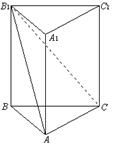18．如图，在直三棱柱ABC—A₁B₁C₁中，AA₁＝2，，，

⑴求证：平面AB₁C⊥平面BB₁C；

⑵求点B到平面AB₁C的距离。

19．如图，在三棱锥P—ABC中，∠ACB＝90º，∠B＝90º，PC⊥平面ABC，AB＝8，PC＝6，

M、N分别是PA、PB的中点，设△MNC所在平面与△ABC所在平面交于直线，

⑴判断与MN的位置关系；⑵求点M到的距离。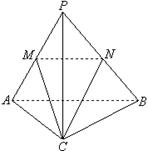

20．如图，△ABC和△DBC所在平面互相垂直，且AB＝BC＝BD，∠ABC＝∠DBC＝120º，

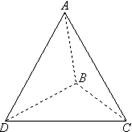求：⑴A、D连线和平面DBC所成的角；⑵二面角A—BD—C的正切值。

21．如图，在四棱椎P—ABCD中，底面ABCD是一直角梯形，∠BAD＝90º，AD∥BC，

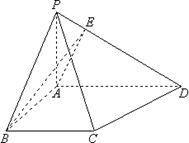AB＝BC＝a，AD＝2a，PD与底面成30º角，PA⊥底面ABCD，

⑴若AE⊥PD于E，求证：BE⊥PD；

⑵求异面直线AE、CD所成角的大小。

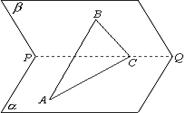
22．如图，已知二面角为60º，点A和点B分别在平面和平面上，点C在棱

PQ上，∠ACP＝∠BCP＝30º，CA＝CB＝a，

⑴求证：AB⊥PQ；⑵求点B到平面的距离；

⑶设R是线段CA上的一点，直线BR与平面所成的角为45º，求线段CR的长度。

数学（十五）（直线、平面、简单几何体1）

参考答案

一、选择题

CBCDD　  BCCAB　　DD

12．提示：BD₁⊥平面AB₁C，EF⊥平面AB₁C

二、填空题

　　　 13．60º　　　　　　　　　 14．7　　　　　　　　　　　　15．1、4、5　　　　　　 16．①、④

三、解答题

17．证明：∵ ∴HG∥AC且

又∵E、F分别是AB、BC中点，∴EF∥AC且，

于是EF∥HG且EF≠HG，四边形EFGH是梯形，FG、EH交于一点P

∵PEH，而EH平面ABD，∴P平面ABD，同理P平面CBD，

故点P在平面ABD与平面CBD的交线BD上

18．⑴由已知条件立即可证得，

⑵在平面BB₁C内作BD⊥B₁C于D，由⑴得BD⊥面AB₁C，

∴BD为B到面AB₁C的距离，∴（本题也可用体积转换）

19．⑴显然可得MN∥平面ABC，∵平面MNC平面ABC＝，∴MN∥

⑵∵PC⊥平面ABC，∴平面PAC⊥平面ABC，作MQ⊥AC，则MQ⊥平面ABC，

作QD⊥于D，则MD⊥，MD的长即为M到的距离

在Rt△ACB中，可求得，又，∠QCD＝30º，

∴，，于是

20．⑴作AO⊥BC交BC的延长线于O，∵面ABC⊥面BCD，∴OA⊥面BCD，连OD，则∠ADO就是AD与平面BCD所成的角，可求得∠ADO＝45º

⑵作OE⊥BD于E，连AE，则BD⊥AE，

∴∠AEO就是二面角A－BD－C的平面角的补角，

∵∠ABO＝60º，∴，，∵∠EBO＝60º，∴

在Rt△AOE中，，∴二面角A－BD－C的正切值为－2

21．⑴∵PA⊥平面ABCD，AB⊥AD，∴AB⊥PD，

又∵AE⊥PD，∴PD⊥平面ABE，故BE⊥PD

⑵设G、H分别为DE、AD的中点，连BH、HG、BG，易知，∴BH∥CD

∵G、H分别为DE、AD的中点，∴GH∥AE，

则∠BHG即为异面直线AE、CD所成的角（或其补角）

而，，，

∴△BHG中，由余弦定理可得异面直线AE、CD所成的角的大小为

（本题也可用建立空间坐标系求解，容易求出，略）

22．⑴在平面内，作BD⊥PQ，连AD，∵∠ACP＝∠BCP＝30º，∴△ACD△BCD

∴AD⊥PQ，PQ⊥平面ABD，则AB⊥PQ，

⑵由⑴知∠ADB是二面角的平面角，∴∠ADB＝60º，

又PQ⊥面ABD，∴⊥面ABD，过B作BE⊥AD于E，则BE⊥，

∴BE为B到平面的距离，可求得

⑶连ER，则∠BRE＝45º，则有

在△ABD中，BD＝AD且∠ADB＝60º，∴

在△ABC中，由余弦定理求得

又在△BCR中，设CR＝x，由余弦定理得

，即

解得，，因，而，故有