直线、平面、简单几何体测试题(三)

直线、平面、简单几何体测试题(三)

(120分钟完卷，总分150分)

一、选择题(本大题共12小题，每小题5分，共60分)

1.四面体每相对的两棱中点连一直线，则此三直线

A.互不相交　　　　　 B.至多有两条直线相交　　　　C.三线交于一点　　D.两两相交有三个交点

2.长方体的长，宽，高分别是3，2,1，从A到沿长方体表面的最短距离是

A.　　　　　　　　　　 B.　　　　　　　　　C.　　　　　　　　 D.

3.正方体中，与截面所成的角是

A.　　　　　　　　　　 B.　　　　　　　　　　 C.　　　　　　　　　　 D.

4.直线m与平面间距离为d，那么到m与距离都等于2d的点的集合是

A.一个平面　　　　　 　　　B.一条直线　　　　　 　　 C.两条直线 　　　　　　　　D.空集

5.若正三棱锥的侧面均为直角三角形，侧面与底面所成的角为，则下列各等式中成立的是

A.0＜＜　　　　　　　 B.＜＜ 　　　　　  C.＜＜ 　　　　 D.＜＜

6.有四个命题：① 当平面到球心的距离小于球半径时，球面与平面的交线总是一个圆；　 ② 过球面上两点只能作一个球大圆；③ 过空间四点总能作一个球； ④ 球的任意两个大圆的交点的连线是球的直径.以上四个命题中正确的有

A.0个　　　　　　　　　　　　　B1个 　　　　　　　　　　　　 C.2个　　　　　　　　　　　　　D.3个

7.一个球与一个正三棱柱的三个侧面和两个底面都相切，已知这个球的体积为，则三棱柱的体积为

A.　　　　　　　　 B.　　　　　 C.　　　 　　　　　D.

8.已知球的直径、长方体对角线、圆柱轴截面对角线均相等，这三种几何体的体积最大值分别是，则有

A. 　　　　　B. 　　　　　C. 　　　　　D.

9.将一个边长为a的正方体，切成27个全等的小正方体，则表面积增加了

A.　　 　　　　 　　　 B.12a²　　 　　　　　　　　　　 C.18a²　　　　　　　　　　　　 D.24a²

10.设正多面体的每个面都是正n边形，以每个顶点为端点的棱有m条，棱数是E，面数是F，则它们之间的关系不正确的是

A.nF=2E 　　　　　　　　　　B.mV=2E　　　　　　　　 　C.V+F=E+2　　　　　　　　　D.mF=2E

11.在底面边长与侧棱长均为a的正三棱柱ABC－A₁B₁C₁中，已知M为A₁B₁的中点，则M到BC的距离是

A.a　　　　　　　　　B.a 　　　 　　　　　 C.a 　　　　　　　 　　 D.a

12.如图，水平地面上有一个大球，现有如下方法测量球的大小，用一个锐角为45°的三角板，斜边紧靠球面，一条直角边紧靠地面，并使三角板与地面垂直，如果测得PA＝5cm，则球的表面积为

A.100πcm²　　　　　　　　　　　 B.100(3＋2)πcm²

C.100(3－2)πcm² D.200πcm²

二、填空题(每小题4分，共16分)

13. 已知正四棱锥S－ABCD的侧面与底面所成的角为60°，过边BC的截面垂直于平面ASD，交平面ASD于EF，则二面角S－BC－E的平面角为　　

14.两个平行于圆锥底面的平面将圆锥的高分成相等的三段，那么圆锥被分成的三部　 分的体积的比是______

15.正三棱锥的底面边长为，侧棱与底面所成角的正弦值为，则此三棱锥的表面积为______

16. 直三棱柱ABC－A₁B₁C₁的体积为9，P、Q分别是侧棱AA₁与CC₁上的点，且AP=C₁Q，则四棱锥B－APQC的体积=　　　

三、解答题(共76分)

17.在长方体中，AB=AD=6，侧棱AA₁=4，E、F、G分别是AB、AD、AA₁的中点.

(1)求证平面EFG//平面B₁CD₁；(2)求异面直线EF与B₁C间的距离.

18.(14分)在直三棱柱ABC－A₁B₁C₁中，CA=CB=1，AA₁=2，，且M，N分别是A₁B₁，A₁A的中点.

(1)求的长；(2)求的值；(3)求证： .

19.(12分）C₇₀ 分子是与C₆₀分子类似的球状多面体结构，它有70个顶点，以每个顶点为一端都有3条棱，各面都是五边形或六边形。求C₇₀分子中五边形和六边形的个数．

20.(12分）正三棱柱ABC—A₁B₁C₁中，AA₁=2AB，D、E分别是侧棱BB₁、CC₁上的点，且EC=BC=2BD，过A、D、E作一截面，求：(1)截面与底面所成的角；（2）截面将三棱柱分成两部分的体积之比.

21.(12分).在四面体ABCD中，AC=m，BD=n，AC与BD成的角为，则异面直线AC与BD间的距离为，求四面体ABCD的体积.

22.(14分)如图，直三棱柱ABC—A₁B₁C₁中，底面是等腰直角三角形，∠ACB=90°，侧棱AA₁=2，D、E分别是CC₁与A₁B的中点，点E在平面ABD上的射影是△ABD的垂心G.

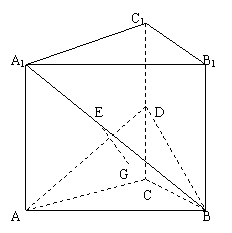(1)求A₁B与平面ABD所成角的大小

（结果用反三角函数值表示）；

　 （2）求点A₁到平面AED的距离.

答　案

1.C 2.C 3.C 4.C 5.D 6.C 7.D 8.C 9.B 10.D 11.A 12.B

13.30⁰

14. 1∶7∶19

15.

16.3

17.(1)略；(2)

18. (1)；(2) ；(3)略.

19. 12，25

20.(1) 45⁰；(2) .3：1

21.略

22. (1)；(2)