高二数学第一学期市区普高期中联考试题
满 分：160分 考试时间：120分钟
命题人：袁贵亮 审 核 人：李干龙
注意：
1、本卷为选物理和选历史的合用卷，分两部分：第一部分为选择题和填空题，所有考生必做；第二部分为解答题，选物理和选历史的有所不同，请注意提示。
2、所有答案都必须填写在答题纸的规定位置。
第一部分
一、选择题（本大题共6小题，每小题5分，共30分。每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确答案的序号填写在答题纸的选择题答题表中。）
1、 如下四个游戏盘 (各正方形边长和圆的直径都是单位1) ，如果撒一粒黄豆落在阴影部分，则可中奖。小明希望中奖，他应选择的游戏盘是……（ ）
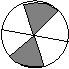
2、3名学生站成一排，其中甲、乙两人站在一起的概率是……（ ）
（A）
（B）
（C）
（D）
3、根据如图所示的伪代码，输出结果为……（ ）
I←1
While I＜8
S←2I+3
I←I+2
End While
Print S
（A）17 （B）19 （C）21 （D）23
4．当x＝0.2时，用秦九韶算法计算多项式
的值时，需要做乘法和加法的次数分别是……（ ）
（A）6，6 （B）5，6 （C）5，5 （D）6，5
5．已知命题P：若
，则x，y都是为0；命题Q：若
，则
，给出下列命题：① P且Q；② P或Q；③ 非P；④ 非Q，其中是真命题的有：……（ ）
（A）① ② （B）① ③ （C）② ③ （D）② ④
6．①某校高二年级共有526人，为了调查学生每天用于休息的时间，决定抽取10%的学生进行调查；②一次数学月考中，某班共有10人在110分以上，32人在90～100分，12人低于90分，现从中抽取9人了解有关情况；③运动会工作人员为参加
×
接力的6支队安排跑道。就这三件事，恰当的抽样方法为：……（ ）
（A）分层抽样、分层抽样、简单随机抽样
（B）系统抽样、系统抽样、简单随机抽样
（C）分层抽样、简单随机抽样、简单随机抽样
（D）系统抽样、分层抽样、简单随机抽样
二、填空题（本大题共10小题，每小题5分，共50分。不需要写出解答过程，请把正确答案填写在答题纸上填空题的相应位置）
7、如图，是一个求50名学生数学平均分的程序，在横线上应填空的语句为
S←0
I←1
While
Read x
S← S + x
I←I+1
End While
A←S/50
Print A
8、实数x，y满足
，则任取其中x，y，使
的概率为
9、已知某设备的使用年限与所支出的维修费用y(万元)，有如下的统计资料：
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若y对x呈线性相关关系，则线性回归方程
表示的直线一定过定点
10、算法的三种基本结构是：顺序结构、 、循环结构。
11、样本为5，6，4，x，8，7的均值为6，方差为 。
12、下面结论中，正确结论的序号为
①命题P：“
”的否定为
:“
”；
②命题：“
”的否定为：“
”；
③若是q的必要条件，则p是
的充分条件；
④“
”是“
”的充分不必要条件。
13、下列关于随机事件的频率与概率的说法正确的有
①频率就是概率；
②频率是客观存在的，与试验次数无关；
③随着试验次数的增多，频率一般会越来越接近概率；
④概率是随机的，在试验前不能确定；
14、抛掷两次骰子，设事件A 为“总数和恰为
15、某人射击一次，命中7～10环的概率如下表所示，则射击1次，命中不足8环的概率是：________________
| 命中环数 | 10环 | 9环 | 8环 | 7环 |
| 概 率 | 0.12 | 0.18 | 0.28 | 0.32 |
16、下面流程图运行的结果是：
↓
↓
↑
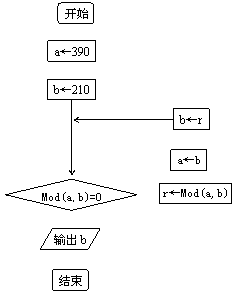
N ↑
→
↓Y
↓
高二数学试题答题纸
得分：________________
第一部分
一、选择题（本大题共6小题，每小题5分，共30分。）
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 答 案 |
二、填空题（本大题共10小题，每小题5分，共50分。）
7、 8、 9、
10、 11、 12、
13、 14、 15、
16、
第二部分
三、解答题：（本大题共6小题，满分80分。解答应写出文字说明、证明过程或演算步骤。）
17、（本小题满分13分）
从标号为A、B、C、D四个相同的小球中任取两个分别放到甲、乙两个盒子中，若每个小球被取到是等可能的，求：
（1）共有多少种放法？
（2）D球恰好放在甲盒中的概率是多少？
（3）A、B两球同时被放到两个盒中的概率是多少？
18、（本小题满分13分）在参加世界杯足球赛的三十二支球队中，随机抽取20名队员，调查其年龄分别为：25，21，23，25，27，29，25，28，30，29，26，24，25，27，26，22，24，25，26，28.
①完成下面的频率布表；
②画出频率分布直方图；
③据此估计全体队员在哪个年龄段的人数最多，占总数的百分之几？
| 分组 | 频数 | 频率 | 频率/组距 |
| 20.5～22.5 | 2 | 0.05 | |
| 22.5～24.5 | |||
| 24.5～26.5 | 8 | 0.2 | |
| 26.5～28.5 | 0.2 | ||
| 28.5～30.5 | 3 | 0.15 | 0.075 |
| 合计 | 20 | 1 | 0.5 |
19、（本小题满分14分）
用循环语句描述求
……
的一个算法，并画出流程图。
20、（本小题满分15分）
如图所示，在边长为4的正方形ABCD的边上有一动点P，沿着折线ADCB由点A（起点）起向点B（终点）运动。设点P运动的路程为x，△APB的面积为y.
①写出y与x之间的函数关系式；
| |
③写出由x求y的伪代码。
P
A B
21、（本小题满分10分）
（1）选历史的考生做:求
有两个同号且不相等实根的充要条件。
（2）选物理的考生做：已知：P:
；q:
(m>0).若P是
的必要不充分条件，求实数的取值范围。
22、（本小题满分15分）
如图，在边长为1的正方形OABC内任取一点P(x,y)
（1）求点P到原点距离小于1的概率；
（2） ①选历史的同学做：以x,y,1为边长能构成三角形的概率；
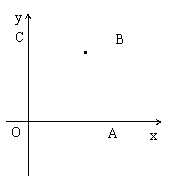②选物理的同学做：以x,y,1为边长能构成锐角三角形的概率。
|
高二数学参考答案
一、选择题：
1.A 2.D 3.A 4.A 5.D 6.D
二、填空题：
7. i≤50 8. π/8 9. (4, 5) 10. 选择结构 11. 5/3
12. ①、③ 13. ③
14. 5
三、解答题
17、（1）共有12种。…………………………………… 5分
（2）D球放到甲盒中包含3个基本事件，概率为3/12=1/4……………… 8分
（3）A、B两球放到盒中包含2个基本事件，概率为2/12=1/6…………… 12分
答：…………………………………… 13分
18、 (1)
| 分 组 | 频 数 | 频 率 | 频率/组距 |
| 20.5～22.5 | 0.1 | ||
| 22.5～24.5 | 3 | 0.15 | 0.075 |
| 24.5～26.5 | 0.4 | ||
| 26.5～28.5 | 4 | 0.1 | |
| 28.5～30.5 | |||
| 合计 |
…………………………………… 5分
(2)
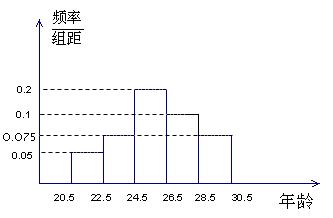
……………11分
(3).在（24.5，26.5）内人数最多，占总数40％。 ………………………13分
19、
|
|
|
|
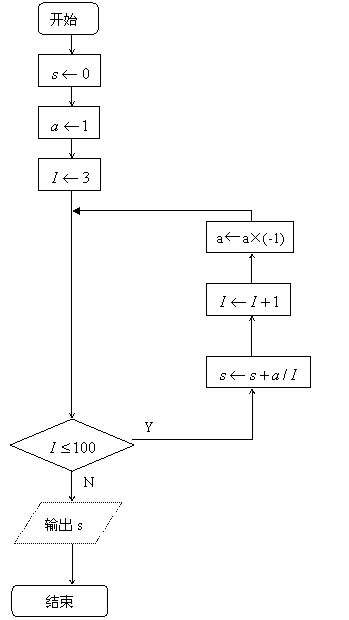
a←1
I←3 ……………… 10分
While I≤100
S← S + a/I
I←I+1
a←a×(-1)
End While ………… 13分
Print S …………… 14分
20．（1） 2x ( 0≤x≤4 )
y= 8 ( 4＜x≤8 ) ……………… 3分
2 (12-x) ( 8＜x≤12 )
(2)
|
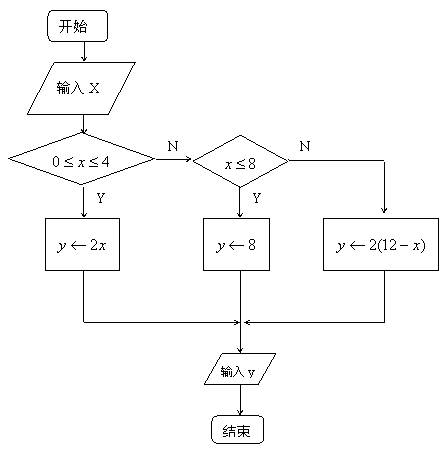
(3) Read x
If 
Then
Else If 
Then
Else
End If
Print y ……………… 15分
21．(历史)
Δ=100－4*3*k>0
充要条件为： ……………… 6分
X1* X2=k/3>0
即: 0＜k＜25/3 …………………………………… 10分
(物理)
P:
； 
………………4分
若P是q的必要不充分条件
则
…………………8分
范围是
…………………………………10分
22．
(1) 所有的点P构成正方形区域D，若点P到原点距离小于1，则
所以符合条件的点P构成的区域是圆
在第一象限所围的平面部分。………5分
点P到原点距离小于1的概率为：
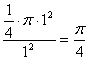…………………………………………………………………………………7分
（2）（历史）
若以x,y,1为边长能构成三角形，则
0<x<1
0<y<1 ………………………………………………………………………………10分
x+y>1
此时点P构成的平面区域是 ABC的内部。……………………………………………13分
概率为：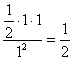
………………………………………………………………14分
答：…………………… 15分
（物理）
构成三角形的点P在 ABC内………………………………8分
若构成锐角三角形，则最大边1所对的角
必是锐角，
，
，……………………11分
即点P在以原点为圆心，1为半径的圆外，
点P在边AB,BC及圆弧AC围成的区域内………………13分
其概率为：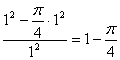
…………………………………14分
答…………………… 15分