高二数学元旦作业
1.下列各式不能化为
的是（ ）
A.
B.
C.
D.
2.已知两点M(3，2)，N(－5,－5)，
=
，则P点坐标是（ ）
A. (－8,1) B. (－1,－
) C. (1, )
D. (8,－1)
3. 在△ABC中，∠C=90°，
则k的值是（ ）
A．5 B．－
D．
4. 若
的夹角为
，且
，则m的值是（ ）
A.0
B.1或
5.已知向量
、
、
满足条件
,
=
==1,则△P1P2P3的形状是( ) A.等腰三角形
B.直角三角形
C.等边三角形
D.不能确定
6.已知向量
,
是不平行于x轴的单位向量,且
,则等于( )
A.(
,)
B.(,) C.(
,
)
D.(1,0)
7. 已知
若
与夹角为钝角，则
的取值范围（ ）
A.
B.
C. 
D.
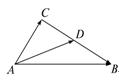8. 已知p=
,q=3,p、q的夹角为
，如图，若
=5p+2q,
=p-3q,D为BC的中点，则
为( )
A.
B.
C.7
D.18
9.已知点A（2，3）、B（10，5），直线AB上一点P满足
，则P点坐标是（ ）A．
B.（18，7） C.或（18，7） D.（18，7）或（－6，1）
10.已知
，
，则
（ ）A 
B 
C 
D 
11. 已知
，则
的值为（ ）A 
B 
C
D
12. 函数
是（ ）
A 周期为的奇函数 B 周期为的偶函数 C 周期为
的奇函数 D 周期为的偶函数
13.求值：
_____________
14.已知=2e1+ke2,
=e1+3e2,
=2e1-e2，若A、B、D三点共线，则k=____________.
15. 若平面向量
与向量
的夹角是
，且
16.
______________
17．已知
，
，若
平行，则λ=
18.已知：
、
、
是同一平面内的三个向量，其中 ＝（1，2）
⑴ 若
，且
，求的坐标；⑵ 若=
且
与
垂直，求与的夹角θ.
19.已知向量
=(3,－4),
=(6,－3),
=(5－m,－3－m).(1)若点A、B、C能构成三角形，求实数m应满足的条件；(2)若△ABC为直角三角形，且∠A为直角，求实数m的值.
20. 已知
求
的值
21.已知函数
（1）求
取最大值时相应的
的集合；（2）该函数的图象经过怎样的平移和伸变换可以得到
的图象
答案
ABACC BDACD BC
13.
14.－8 15.(－3,6) 16.
17.
18.(1)
或
(2)
19. (1)实数m≠时满足条件. (2) m=
20.
21.(1)
(2)纵坐标变为原来的
倍，再横坐标变为原来的倍，再向右平移
个单位
5.解析：由
=0,得
.
∴
=
=
.∴()2=
,
即
.
由
=1,得·=-.
同理,可得·=·=
.
又
，∴
2=
·
=1+1+1=3.
同理,
=
,=,∴=
=
=.∴△P1P2P3是正三角形.
6.解析：b为单位向量,∴设b=(cosθ,sinθ).
∵a·b=,∴(,1)·(cosθ,sinθ)=cosθ+sinθ=.
∴sin(θ+)=sin.∴θ+=或θ+=π-.∴θ=0或θ=.
当θ=0时,b=(1,0),b∥x轴,不合题意舍去. 当θ=时,b=(,).
8.解析：=(
)=(5p+2q+p-3q)=(6p-q)，
∴=
=
=
=
=.
14.解析：若A、B、D三点共线，则∥
，设
=λ
.
∵
=e1-4e2，∴2e1+ke2=λ(e1-4e2)=λe1-4λe2.∴
∴k=－8.
19.解：(1)已知向量=(3,－4),
=(6,－3),
=(5－m,－3－m)，
若点A、B、C能构成三角形，则这三点不共线.
∵
∴3(1－m)≠2－m.
∴实数m≠时满足条件.
(若根据点A、B、C能构成三角形，则必须AB+BC＞CA)
(2)若△ABC为直角三角形，且∠A为直角，则⊥，
∴3(2－m)＋(1－m)=0，解得m=