高中数学必修3学习质量评估试卷
参考公式:b=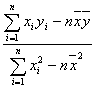 ,a=
,a=![]() -b
-b![]() ,b是回归直线的斜率,a是截距
,b是回归直线的斜率,a是截距
Ⅰ、选择题(3分×13=39分)
1.算法是指可以用计算机来解决的某一类问题的程序或步骤,它不具有( )
A.有限性B.明确性C.有效性D.无限性
2.程序框图是算法思想的重要表现形式,程序框图中不含( )
A.流程线B.判断框C.循环框D.执行框
3.程序框图中有三种基本逻辑结构,它不是( )
A.条件结构B.判断结构C.循环结构D.顺序结构
4.下列程序语句不正确的是( )
A.INPUT“MATH=”;a+b+c B.PRINT“MATH=”;a+b+c
C.a=b+c D.a1=b-c
5.抽样调查时,为了反映样本的代表性,对总体进行随机抽样,样本必须符合()
A.等可能性B.有限性C.分层性D.可靠性
6.与标准差单位不一致的是( )
A.平均数B.相关系数C.众数D.中位数
7.在教学调查中,甲、乙、丙三个班的数学测试成绩分布如图:
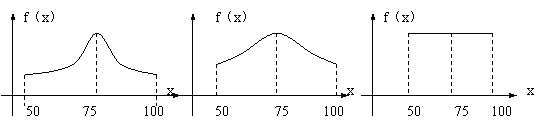
设75分是各班的平均分,![]() 分别表示甲、乙、丙三个班数学测试成绩的标准差,则有( )A.
分别表示甲、乙、丙三个班数学测试成绩的标准差,则有( )A.![]() B.
B.![]() C.
C.![]() D.s3>s2>s1
D.s3>s2>s1
8.某班有60名学生,近视者有45名,体检中医生检查该班前5名都是近视者,检查第6名学生仍是近视者的概率为( )
A.![]() B.
B.![]() C.
C.![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() D.
D.![]()
9.x1是[0,1]内随机数,x是[-1,1]内的随机数,则x1与x之间的关系是( )
A.x1=2x-1 B.x=2(x1-1) C.x=2x1-1 D.x1=2(x-1)
10.在程序框图中一般不含有条件判断框的结构是( )
A.顺序结构B.循环结构C.当型结构D.直到型结构
11.下表是十六进制与十进制转化表
| 16进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 10进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
已知在十六进制中A×B=6E,则D×E为 ( )
A 116 B 6B C 611 D B6
12.通过求Q=![]() 2的最小值而得到回归直线的方法称为()
2的最小值而得到回归直线的方法称为()
A.辗转相除法B.随机模拟法C.秦九韶法D.最小二乘法
13.连掷两次骰子得到的点数分别为m和n,则向量a=(m,n)与向量b=(1,-1)数量积大于0的概率为( )
A.![]() B.
B.![]() C.
C.![]() D
D![]()
Ⅱ、填空题(4分×5=20分)
14.某比赛为两运动员制定下列发球规则:
规则一:投掷一枚硬币,出现正面向上,甲发球,反面向上,乙发球;
规则二:从装有2个红球与2个黑球的布袋中随机地取出2个球,如果同色,甲发球,否则乙发球;
规则三:从装有3个红球与1个黑球的布袋中随机地取出2个球,如果同色,甲发球,否则乙发球;
则对甲、乙公平的规则是______
| |
16.在程序语句中,赋值语句s=s+i起累加作用,类似地起累乘作用的赋值语句是________
17.若集合M={0,l,2},N={(x,y)x-2y+1≥0且x-2y-1≤0,x,y ∈M},由M中数为坐标的点随机地撒在平面直角坐标系上,落在N区域内的概率为____
18.若以连续掷三次骰子分别得到的点数![]() ,p作为点Q的坐标,则点Q落在以原点为球心,3为半径的球面内(含球面)的概率是_____
,p作为点Q的坐标,则点Q落在以原点为球心,3为半径的球面内(含球面)的概率是_____
Ⅲ、解答题(41分)
19.(12分)两学生在高中三年的数学测试成绩如下:
甲:89,91,86,79,93,88,96,78,95,89,87,88
乙:67,88,92,95,77,85,69,79,83,99,68,73
试写出它们的茎叶图,简单分析谁的成绩比较稳定。
20.(14分)某班学生高考数学成绩与会考数学成绩数据如下:
| 会考数学成绩 | C | B | A | A |
| 会考数学量化成绩 | 5 | 7 | 10 | 10 |
| 高考数学简化成绩 | 0 | 15 | 28 | 39 |
| 高考数学成绩 | 100 | 115 | 128 | 139 |
(1)根据会考数学量化成绩与高考数学简化成绩,画出后者相对于前者的散点图;
(2)写出高考数学简化成绩相对于会考数学量化成绩的回归直线方程。
21.(15分)已知n次多项式![]() ,
,
如果在一种算法中,计算![]() (k=2,3,4,…,n)的值需要k-1次乘法,
(k=2,3,4,…,n)的值需要k-1次乘法,
(1)计算![]() 的值需要9次运算(6次乘法,3次加法),那么计算
的值需要9次运算(6次乘法,3次加法),那么计算![]() 的值需要多少次运算?
的值需要多少次运算?
(2)若采取秦九韶算法:![]() (k=0, 1,2,…,n-1),计算
(k=0, 1,2,…,n-1),计算![]() 的值只需6次运算,那么计算
的值只需6次运算,那么计算![]() 的值共需要多少次运算?
的值共需要多少次运算?
(3)若采取秦九韶算法,设ai=i+1,i=0,1,…,n,求P5(2)(写出采取秦九韶算法的计算过程)
答案:
1.D;2.C;3.B;4.A;5.A;6.B;7.D;8.C;9.B;10.C;11.B;12.D;13.A
14.规则一和规则三;;15.![]() 16.t=t*i;17.
16.t=t*i;17.![]() ; 18.
; 18. ![]()
19.
| 甲 | 乙 | |
| 6 | 7 9 8 | |
| 8 9 | 7 | 7 9 3 |
| 9 6 8 9 7 8 | 8 | 8 5 3 |
| 1 3 6 5 | 9 | 2 5 9 |
甲的成绩基本上对称,叶的分布呈“单峰”,且从叶在茎上的分布看,甲的成绩比较稳定
20.(1)画散点图(略)
(2)
| 会考数学量化成绩x | 高考数学简化成绩y | x2 | xy | |
| 1 | 5 | 0 | 25 | 0 |
| 2 | 7 | 15 | 49 | 105 |
| 3 | 10 | 28 | 100 | 280 |
| 4 | 10 | 39 | 100 | 390 |
| 总和 | 32 | 82 | 274 | 775 |
![]() =8,
=8,![]() =20.5
=20.5
b=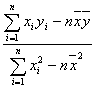 =
=![]() =6.61 a=
=6.61 a=![]() -b
-b![]() =-32.38
=-32.38
∴回归直线为y=6.61x-32.38
21.(1)![]() n(n+3)(2)2n;(3)∵
n(n+3)(2)2n;(3)∵![]() ,
,
∴P0(2)=1,P1(2)=2P0(2)+2=4;P2(2)=2P1(2)+3=11;
P3(2)=2P2(2)+4=26;P4(2)=2P3(2)+5=57;P5(2)=2P4(2)+6=120