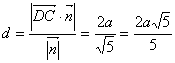立体几何中的向量方法
备课：余乃灵
在立体几何的学习中，求各种“空间角”、和空间“距离”的难点在于作出相应的“角”及作出表示“距离”的线段，并给出相应的证明。引入向量的工具，避开了“作”、“证”这个难点，提供了解决求空间角、距离及证明“垂直”、“平行”的通法。进一步强化了“坐标法”、“数形结合”和“转化”等数学思想方法.
复习过程与方法：
1. 立足课本，掌握好向量的相关知识：概念、基本运算、建系方法、坐标求法（不定点的坐标）、平行与垂直、法向量求法
2. 掌握向量作为工具解决立几问题的方法
3.
 |
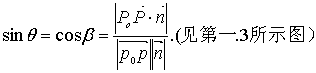向量解题后建议多思考传统的方法，不仅可以锻炼思维能力，还可以深刻认识空间几何的本质
相关知识与能力：
一.空间距离的计算
1. 空间两点间的距离：设A、B是空间两点，则A、B两点间的距离d=
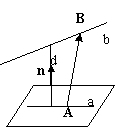2.两条异面直线间的距离：设a、b是两条异面直线，
是a、b的公共法向量（即
），点AÎa,BÎb
则异面直线a、b间的距离
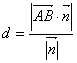
即
方向上的射影长为异面直线a、b间的距离。
3.点（或线）到平面的距离：
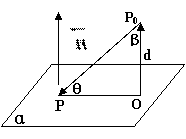1）设
P是平面α内任一点，则PO到平面α的距离
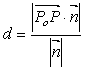
2)直线与平面（或平面与平面）的距离转化为点到平面的距离。
二.空间角度的计算
1. 两条异面直线所成的角：设l1与l2两条异面直线，∥l1 ， 
∥l2，则l1与l2所成的角
α=<，>或α=л
-<，> （0<α≤
）
cos<，>=
或 cosα=
（0<α≤）
2. 斜线P0P与平面α所成的角θ
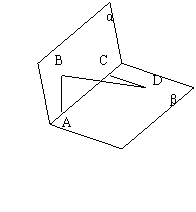3.二面角：设相交平面α与β的法向量分别为
，则α与β所成的角的大小为<> 或 
（如何确定？）
基础演练：
1.(1).二面角α-l-β的大小
是120o,A、CÎl,BÎα,
且AB⊥l,CD⊥l,AB=CD=a,
AC=2a。求BD的长。
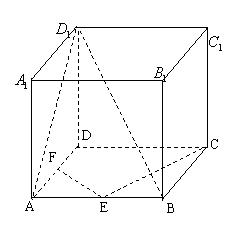(2) 二面角α-l-β,A、CÎl,
BÎα,且AB⊥l,CD⊥l,
AB=CD=a,AC=2a,BD=
,
求二面角α-l-β的大小.
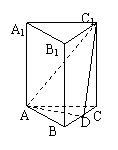
2.正方体
中，E、F分别为
、
的中点，
(1)
与
所成角
(2) 与
所成角
(3) 
与
所成角
(4)与所成角
(5)
与
所成角； (6)与平面
所成角
(7)与平面
所成角; (8)二面角
的大小; (9)二面角
的大小;
(10)二面角
的大小; (11)
的长度；
（12）C到ABD1的距离; (13)四面体EFBC1的体积;
(14)异面直线EC,AD1的距离;
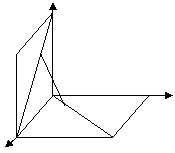
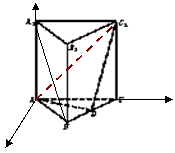
3.如图正三棱柱，棱都相等，
D是BC的中点.若AB=2。
1） 求证A1B∥平面ADC1。
2）求A1B与截面ADC1的距离
巩固提高
|
1. 如图，正方形
、
的边长都是1，而且平面、互相垂直。点
在
上，点
在
上，若
求MN与BE所成角的余弦值。
2.直三棱柱ABC－A1B1C1中，
AA1＝2，AB＝AC＝1，
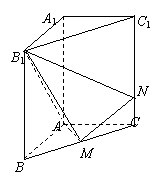∠BAC＝900，已知点M是
BC的中点，点N在侧棱CC1上.
(Ⅰ).当线段CN的长度为多少
时，MN⊥AB1；
(Ⅱ).若MN⊥AB1，求B1N与
平面AB1M所成角的余弦值
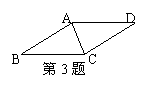
3.在平行四边形ABCD中，
AB=AC=1，∠ACB=900,将
它沿对角线AC折起，使AB
与CD成600角，求B、D间距离。
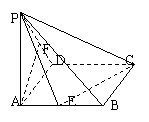
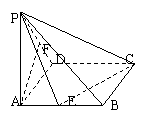4.已知四棱锥P—ABCD的底面为正方形，PA⊥底面ABCD，E、F分别为AB、PD的中点，PA=a，二面角P—CD—B为45°。
（1）求证：AF∥平面PCE；（2）求证：平面PCE⊥平面PCD；（3）求点D到平面PCE的距离.
 |
基础演练：
1.（1）；（2）1200
2. （1）
（2）
（3）（4） （5）
（6）
（7）
（8）（9）
（10）
3解：1) 建立空间直角坐标系A-xyz
则：A（0，0，0），B（
，1，0）
C（0，2，0），C1（0，2，2），A1（0，0，2）
∴D
∴
设平面ADC1的法向量为
从而有：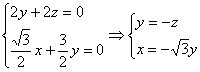
取
∵
又 A1BË平面ADC1
∴A1B∥平面ADC1
2)由1）知，A1B∥平面ADC1，
所以A1B与截面ADC1的距离等于A1点到截面ADC1的距离
∵
∴
∴
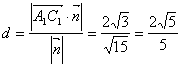
故A1B与截面ADC1的距离等于
巩固提高：
1. 解1：由条件知：BA、BC、BE三线两两垂直
成以可建直角坐标系如图所示
∵CM=1
∴
∴
|
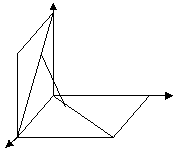同理：
∴
Þ
又
Þ
∴
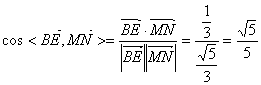
故MN与BE所成角的余弦值为
注：求点M的坐标用到了空间定比分点坐标公式：
2.（Ⅰ）CN＝
时，MN⊥AB1；（Ⅱ）
3.
4. （1）∵底面是正方形，∴AD⊥CD
又PA⊥底面AC，∴PD⊥CD（三垂线定理）
∴∠PDA=45°∴AD=PA=a
建立直角坐标系（如图所示）
则易得：A（0，0，0）B（a，0，0）
|
又E、F分别是AB、PD的中点
∴
设平面PCE的法向量为
则由
∴
又AFË平面PCE，故AF∥平面PCD
（2）易得
得法向量为
，又由（1）知：
∴
从而平面PCE⊥平面PCD。
（3）∵
∴求点D到平面PCE的距离
