数列的概念与方法训练题

数列的概念与方法训练题

一、选择题：

1．数列1，3，6，10，……的一个通项公式是（　　）

A．n²－n+1　　　　　B．　 　　　　C．n(n－1)　　　　　D．

2．已知数列的通项公式为a_n=n(n－1),则下述结论正确的是　　　　（　　）

A．420是这个数列的第20项　　　　　　　　　 B．420是这个数列的第21项

C．420是这个数列的第22项　　　　　　　　　 D．420不是这个数列中的项

3．在数列{a_n}中，已知a₁=1,a₂=5, a_n+2=a_n+1－a_n,则a₂₀₀₀=　　　　（　　）

A．4　　　　　　　　B．5　　　　　　　　　　C．－4　　　　　　　D．－5

4．设数列{a_n}的首项为1，对所有的n≥2，此数列的前n项之积为n²，则这个数列的第3项与第5项的和是 (　 )

A．　　　　　　　B．　　　　　　　　　C．　　　　　　　D．

5．在数列{a_n}中，均为正实数，则a_n与的大小关系是（　　）

A．a_n <　　　　 B．a_n >　　　　　　 C．a_n =　　　　 D．不能确定

6．数列{a_n}的前n项和　　 （　　）

A．(2ⁿ－1)²　　　　　B．(2ⁿ－1) 　　　　　　C．4ⁿ－1 　　　　　　D．(4ⁿ－1)

二、填空题：

7．数列{a_n}中，a₁=3,  a_n+1=a_n+2ⁿ+3，则a_n= 　　　　　　　 

8．已知数列{a_n}满足：a₁=1, a_n= a_n－1+ a_n－2+…+ a₂+ a₁（n≥2），则该数列的通项公式a_n=　　　　　　　　　

9．已知{a_n}的前n项和S_n=n²－4n+1,则a₁+a₂+…+a₁₀的值为　 　　　　　　 

10．已知{a_n}中，a₁=1, a_n=，则a₁₂=　　　　　　　　　　   

三、解答题

11．已知数列{a_n}的前n项和为，数列{b_n}的前n项和为T_n=3n²－2n+1，

　 （I）若a₁₀=b₁₀，求p的值；

　 （II）取数列{b_n}的第1项，第3项，第5项，…，第2n－1项，…作一个新数列{c_n}，求数列{c_n}的通项公式.

12．设数列{a_n}的首项为1，前n项和为S_n与通项a_n之间满足：

（I）求证：数列是等差数列；（II）求数列{a_n}的通项公式.

13．已知数列{a_n}的前n项和为S_n，a₁=1,且对一切正整数n有2 S_n=(n+p) a_n,p为常数,

　 （I）求p值；　（II）求数列{a_n}的通项公式.

14．已知数列{a_n}的前n项和N*），试讨论数列{a_n}的单调性.

15．设数列{a_n}的各项为正数，若对任意的正整数n, a_n与2的等差中项等于其前n项和S_n与2的等比中项，求{a_n}的通项公式.

参考答案与解析

　　一、1．D　2．B　3．B　4．C　5．A　6．D

　　二、7．2ⁿ+3n－2　　8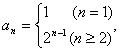．　　9．67,　　 10．.

11．(I)由a₁₀=b₁₀得p=36；

　　（II）当n≥2时，

12．（I）当n≥2时，由

　　是公差d=2，首项的等差数列；

　 （II）∵

13．（I）取

　　

14．当

　　

　  

　　∴对n∈N*有a_n+1>a_n ,即{a_n}为单调递增数列.

15．