高二文科数学期末模拟试卷
总分150分
一、选择题
1.设![]() ,则下列不等式中不成立的是( )
,则下列不等式中不成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.在![]() 中,根据下列条件解三角形,其中有两个解的是( )
中,根据下列条件解三角形,其中有两个解的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.一位母亲记录了儿子3—9岁的身高,数据(略),由此建立的身高与年龄的回归模型为
![]() ,用这个模型预测这个孩子10岁时的身高,则正确的叙述是( )
,用这个模型预测这个孩子10岁时的身高,则正确的叙述是( )
A.身高在
C.身高一定是
4.等差数列![]() 中,
中,![]() ,则前10项的和
,则前10项的和![]() ( )
( )
A.100 B
5.椭圆![]() 的焦点坐标是( )
的焦点坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.椭圆![]() 的两个焦点为
的两个焦点为![]() ,过
,过![]() 作垂直于
作垂直于![]() 轴的直线与椭圆相交于
轴的直线与椭圆相交于![]() 两点,则
两点,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.4
D.4
7.函数![]() 的单调递减区间为( )
的单调递减区间为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.若双曲线的渐近线方程为![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.![]() B.
B.![]() C.
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
9.已知命题![]() 若实数
若实数![]() 满足
满足![]() ,则
,则![]() 全为0.
全为0.
命题![]() 若
若![]() ,则
,则![]() .
.
①![]() 为真; ②
为真; ②![]() 为真 ③
为真 ③![]() 为真 ④命题
为真 ④命题![]() 的否定为真
的否定为真
上述:①,②,③,④中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
10.在![]() 上定义运算
上定义运算![]() ,若不等式
,若不等式![]() 对任意实数
对任意实数![]() 成立,则实数
成立,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
11.命题“![]() ”的否定是 ________
_ 。
”的否定是 ________
_ 。
12.已知抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,![]() 是抛物线上一点,则
是抛物线上一点,则![]() 的最小值为
。
的最小值为
。
13.设![]() 为正数, 则
为正数, 则![]() 的最小值为
。
的最小值为
。
14.已知抛物线型拱桥的顶点距水面![]() ,测量水面宽度为
,测量水面宽度为![]() ,当水面上升
,当水面上升![]() 后,水面宽度为
后,水面宽度为
![]() 。
。
15.物体所经过的路程![]() (单位:
(单位:![]() )与运动时间在
)与运动时间在![]() (单位
(单位![]() )满足方程
)满足方程![]() 中,那么物体在
中,那么物体在![]() 时的瞬时速度
时的瞬时速度![]() ________
________![]() 。
。
16.数列![]() ,的前
,的前![]() 项之和等于
。
项之和等于
。
三、解答题
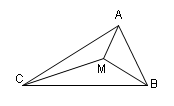 17.已知
17.已知![]() 是
是![]() 内一点,
内一点,![]() ,求
,求![]() 的长度。
的长度。
18.某工厂可以生产两种不同原料生产的同一种产品,若采用甲原料,每吨成本1000元,运费500元,可得产品90千克;若采用乙种原料,每吨成本1500元,运费400元,可得产品100千克。现在预算每日总成本不得超过6000元,运费不得超过2000元,问此工厂每日最多可生产多少千克产品?
19.已知等差数列![]() 的前
的前![]() 项和为
项和为![]()
①求![]() 的值;
的值;
②若![]() 与
与![]() 的等差中项为18,
的等差中项为18,![]() 满足
满足![]() ,试证明
,试证明![]() 是等比数列,并求
是等比数列,并求![]() 的前
的前![]() 项和。
项和。
20.已知函数![]() 在
在![]() 处有极值,其图象在
处有极值,其图象在![]() 处的切线与直线
处的切线与直线![]() 平行.
平行.
①求函数的单调区间;
②求函数的极大值与极小值的差;
③当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
21.已知椭圆![]() 与过点
与过点![]() 的直线
的直线![]() 有且只有一个公共点
有且只有一个公共点![]() ,且椭圆的离心率
,且椭圆的离心率![]() ,
,
①求椭圆方程;
②设![]() 分别为椭圆的左、右焦点,
分别为椭圆的左、右焦点,![]() 为线段
为线段![]() 的中点,求证:
的中点,求证:![]() 。
。
高二文科数学期末模拟试卷参考答案
一、选择题 BDABC CACBC
二、填空题 ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
; ![]()
三、解答题
17.解:在![]() 中,由正弦定理,
中,由正弦定理,![]()
在![]() 中,
中,![]() ,
,
由余弦定理,![]() ,故
,故![]()
18.解:设分别采用甲、乙两种原料各![]() 千克,可生产产品
千克,可生产产品![]() 千克,
千克,
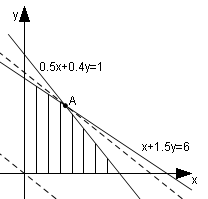 依题意,约束条件为
依题意,约束条件为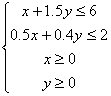
目标函数为![]()
![]() 把目标函数化为
把目标函数化为![]() ,当直线
,当直线![]() 的纵截距取最大值时,
的纵截距取最大值时,![]() 也取最大值。画出可行域如右图。在可行域中平移直线
也取最大值。画出可行域如右图。在可行域中平移直线![]() ,当直线过点
,当直线过点![]() 时,
时,![]() 取最大值。由
取最大值。由![]() ,解得
,解得![]() ,
,
此时![]()
答:分别采用甲、乙两种原料各![]() 千克,可生产最多的产品
千克,可生产最多的产品![]() 。
。
19.解:①![]()
当![]() 时,
时,![]()
故![]()
由![]() ,得
,得![]() ,解得
,解得![]()
②证明:![]()
又由①,![]() ,所以
,所以![]()
![]() ,得
,得![]() ,
,![]()
故数列![]() 是以
是以![]() 为公比的等比数列,且首项
为公比的等比数列,且首项![]()
于是![]()
20.解:![]() ,由该函数在
,由该函数在![]() 处有极值,
处有极值,
故![]() ,即
,即![]() ………………①
………………①
又其图象在![]() 处的切线与直线
处的切线与直线![]() 平行
平行
故![]() ,即
,即![]() ………………②
………………②
由①,②,解得![]()
所以![]() ,
,![]()
①令![]() ,解得
,解得![]() 或
或![]() ;令
;令![]() ,解得
,解得![]()
故该函数的单调递增区间为![]() 和
和![]() ,而递减区间为
,而递减区间为![]()
②结合①的结果可有如下表格:
|
|
| 0 |
| 2 |
|
|
| + | 0 | - | 0 | + |
|
|
| 极大值 |
| 极小值 |
|
于是,当![]() 时,
时,![]() 有极大值为
有极大值为![]() ;当
;当![]() 时,
时,![]() 有极小值为
有极小值为![]()
故函数的极大值与极小值的差为4
③当![]() 时,
时,![]() ,则
,则![]() 在区间
在区间![]() 上的最小值大于
上的最小值大于![]()
结合②的结果,![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]()
故![]() ,解得
,解得![]() 或
或![]()
21.解:①过点![]() 、
、![]() 的直线方程为
的直线方程为![]()
由题意得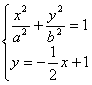 有惟一解,
有惟一解,
即![]() 有惟一解,
有惟一解,
所以![]() (
(![]() ),
),
故 ![]()
又因为 ![]() 即
即 ![]() 所以
所以 ![]()
从而得 ![]() 故所求的椭圆方程为
故所求的椭圆方程为![]()
②由①得 ![]() 故
故![]() 从而
从而![]()
由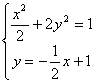 ,解得
,解得![]() ,所以
,所以![]()
因为![]() 又
又![]()
![]() 得
得
注意到![]() ,
,
故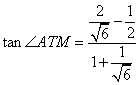
![]()
因此![]()