高二文科数学下学期期中试卷（）
班级 姓名 学号
时间:120分钟 满分:120分 命题人：刘金荣
一、选择题：（本大题共10小题，每题4分，共计40分）
1、直线y=
x+1的倾斜角为
( )
A. 150º
B. 60º C.120º D. 
2、直线2x-y+1=0与直线x+2y-5=0的位置关系是：( )
A、平行 B、重合 C、垂直 D、相交但不垂直
3、若
，则
，
，
，
中最大一个是（ ）
A． B．
C． D．
4、不等式
<
2的解集是：（ ）
A、{xx>
} B、{xx<0} C、{xx<0或x>} D、{x0<x<}
5、已知函数
（x>0），则函数的最小值为是（ ）
A．-4 B．
6、已知点(1,1)到直线L：3x+4y+8=0的距离为（ ）
A. 1
B.
7、已知直线y=x 和直线y=kx+1若两直线的夹角为60º,则 k 的值为（ ）
A. －或 0 B.－
C.或 0 D. 0
8、用一段长为Lm的篱笆围一个一边靠墙的矩形菜园，菜园的最大面积为 （ ）
A. 
m2 B.
m
m2 D.
m2
9、下列的点在不等式：
表示的区域内的是（ ）
A．（0，0） B.(1,1) C.(-1,0) D.(0,-1)
10、经过两直线ｘ＋３ｙ＋１０＝０和ｙ＝３ｘ的交点，且与原点距离为１的直线方程
是（ ）
Ａ.３ｘ－４ｙ－５＝０或ｘ＝－１ Ｂ.４ｘ－３ｙ－５＝０或ｘ＝１
Ｃ.３ｘ－４ｙ－５＝０或ｘ＝１ Ｄ.４ｘ－３ｙ－５＝０或ｘ＝－１
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二、填空题：（本大题共5小题，每题4分，共20分，把答案填在题中的横线上）
11、点P（1，0）关于直线 y=x 的对称点坐标是 _____ __ 。
12、将直线
绕点(1 , 0)顺时针旋转
所得的直线的一般方程式是__________。
13、经过
两点的直线的斜率是___________.
14、已知
，且x+y=1，则
的最小值是_________。
15、设
满足约束条件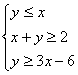
则使得目标函数
的最小值为 。
三、解答题：（本大题共6小题，计60分，解答应写出文字说明，证明过程或演算步骤）
16、（本小题满分10分）解不等式
。
18、（本小题满分10分）已知一条直线通过点Ｐ（１，２）且与直线ｘ＋ｙ＋６＝０的夹角为
，求这条直线的方程。
19、（本小题满分10分）已知直线L在x、y轴上的截距相等，且经过点A（2，1），求直线L的方程。
20、（本题满分10分）
某工厂计划用甲，乙两台机器生产A，B两种产品，每种产品都要依次进行甲、乙机器的加工，已知生产一件A产品在甲、乙机器上加工的时间分别为2小时和3小时，生产一件B产品在甲、乙机器上加工的时间分别为4小时和2小时，甲、乙机器每周可分别工作180小时和150小时，若每件A产品的利润是40元，每件B产品的利润是60元，问此工厂应如何安排生产才能获得最大的利润（即如何确定一周内每种产品生产的数量）
21、（本题满分10分）已知函数y=f(x)的定义域为[-1,1],对任意
都有
，且f(1)=1,若m,n∈[-1,1],m+n≠0时,有
(1)用定义证明f(x)在[-1,1]上是增函数
(2)解不等式:
(3)若f(x)≤t2-2t+1,对所有x∈[-1,1]恒成立,求实数t的范围
高二文科数学下学期期中试卷
高二数学试题参考答案及评分标准
一、选择题（本大题共10小题，每题4分，共计40分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | A | C | C | C | A | D | A | D |
二、填空题：（本大题共4小题，每题4分，共16分）
11、（0，1）； 12、x-y-1=0; 13 -1; 14、4; 15、3.
三、解答题：
16、（-2，-1）或（1，2）
17、（本小题满分8分）
①ａ≠３且ａ≠－１；②ａ＝
；③ａ＝－１④ａ＝３
18、（本小题满分10分）
解：当所求直线斜率存在时设它为ｋ，则由夹角公式有
═> ｋ＝０ ═> ｙ＝２为所求
当所求直线斜率不存在时，过点（１，２）的直线方程为ｘ＝１
此时两直线的夹角也是，故所求直线的方程是：ｘ＝１和ｙ＝２
19、（本小题满分10分）
解：当L过原点时，方程为：y=2x;
当L的斜率为-1时，方程为：y=-x+3.
20、（本小题满分10分）
解：设A，B两种产品一周的产量分别为 x 件y件总利润为S，则 2x+
4y 
180
3x+2y 150
x 
0 ,y 0 ----------- 4分，作出可行域（图略）---------6
目标函数为s=40x+60y 作直线L:40x+60y=0 把L向右上方移至过2x+4y=180与3x+2y=150 交点,M(30,30)处时，L与原点的距离最大
---------------------8
此时s=40x+60y 取得最大值为3000. --------------------9
因此每周生产A，B 产品均为 30 件时，工厂可获的最大利润300 元 。 10
21、（本小题满分10分）酌情给分