高二月考数学试题

高二月考数学试题

总分150分

一．选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。）

1．关于频率分布直方图，下列有关说法正确的是　　　　　　　　　　　　  （　D　）

A．直方图的高表示取某数的频率。

B．直方图的高表示该组上的个体在样本中出现的频率。

C．直方图的高表示取某组上的个体在样本中出现的频数与组距的比值。

D．直方图的高表示取该组上的个体在样本中出现的频率与组距的比值。

2．下列说法错误的是 (　 C　)

A．命题“若 则 ”的逆否命题为：“若, 则”。

B．“”是“”的充分不必要条件。

C．若为假命题，则．均为假命题。

D．对于命题：使得. 则： 均有。

3．若函数f（x）=2x²－1的图象两点（1，1）及（1+Δx，1+Δy），则等于（　C ）　 

A．4　　　　　　　　 B．4x　　　　　　　　　　　　　　　 C．4+2Δx　　　　　  D．4+2Δx²

3．已知点A(1, -2, 11)，B(4, 2, 3)，C(6, -1, 4)，则△ABC的形状是　　　　　　　　　  （　C  ） 　

　 A．等腰三角形　　　 B．正三角形　　   C．直角三角形　　  D．等腰直角三角形

4．椭圆的短轴长为2，长轴是短轴的2倍，则椭圆的中心到其准线的距离是　（　D  ）

A．　　　　　 B．　　　　　C．　　　　　 D．

5．曲线y=x³－3x²+1在点（1，－1）处的切线方程为　　　　　　 （　A  ） 　

A．y=－3x+2 　　　　 B．y=3x－4　　C．y=－4x+3 　　　　　 D．y=4x－5

5．已知四面体ABCD中，AB，AC，AD两两互相垂直，给出下列命题：

①；②；

则下列关于以上两个命题的真假性判断正确的是　　　　　　　　　　　　　 （　A　）

A．①真②真　　　 B．①假②真　　　　 C．①假②假　　　　  D．①假②真

6．已知动点P（x,y）到点（1，2）的距离等于到直线3x+4y-11=0的距离，则P点的轨迹是　　 （ A ）

A．直线　　　 B．抛物线　　　　  C．双曲线　　　　 D．椭圆

7．若抛物线的焦点与椭圆的右焦点重合，则的值为　　　　（　B  ）

A． 　　　　 B．　　　　  C．　　　　　　　  D．

8．过点(0,1)作直线，使它与抛物线仅有一个公共点，这样的直线有　 （　C　 ）

A.1条　　B.2条　　C. 3条　 D. 0条

9．双曲线的渐近线方程为，则双曲线的离心率为　　　　　　　 （　D　 ）

A．　　　　　 B．　　　　  C．或　　　　D．

10．下面有三个游戏规则，袋子中分别装有球，从袋中无放回地取球，问其中不公平的游戏是（D）　　　　　　　　　　　　　　　　　　　　　　　　　　  　　　　　　　　 

游戏1	游戏2	游戏3
3个黑球和一个白球	一个黑球和一个白球	2个黑球和2个白球
取1个球，再取1个球	取1个球	取1个球，再取1个球
取出的两个球同色→甲胜	取出的球是黑球→甲胜	取出的两个球同色→甲胜
取出的两个球不同色→乙胜	取出的球是白球→乙胜	取出的两个球不同色→乙胜

A. 游戏1和游戏3　　　 B. 游戏1　　　　 C. 游戏2　　　　  D.　游戏3

二．填空题（本大共6小题，每小题6分，共36分）

11．写出命题：“，使=0”的否定。

12．下列程序：

　　Read　

　　 For　I  from　1　to  5　step　2

　　　　 

　　　　　　 print

End　 for

End

输出的结果是 　　2，8，48　 。

13．一动点到y轴的距离比到点(2，0)的距离小2，这个动点的轨迹方程是_______

答案：y²=8x或y=0（x<0）

14．设函数f（x）=（x－a）（x－b）（x－c）（a．b．c是两两不等的常数），则++=___0__。

解析：∵f（x）=x³－（a+b+c）x²+（ab+bc+ca）x－abc，

∴（x）=3x²－2（a+b+c）x+ab+bc+ca.

又（a）=（a－b）（a－c），同理（b）=（b－a）（b－c），

（c）=（c－a）（c－b）.

代入原式中得值为0.

14．已知实数满足，则　 4　　。

15．若双曲线的右支上一点P（a,b）直线y=x的距离为，则a+b 的值是　  

16. 为了科学地比较考试的成绩，有些选拔性考试常常将考试分数转化为标准分，转化关系式为（其中是某位学生的考试分数， 是该次考试的平均分，s是该次考试的标准差，Z称为这位学生的标准分），转化成标准分后可能出现小数或负数，因此，又常常再将Z分数作线性变换转化成其他分数。例如某次学业选拔考试采用的是T分数，线性变换公式是：，已知在这次考试中某位考生的考试分数是85，这次考试的平均分是70，标准差是25，则该考生的T分数为_______84_____.

三．解答题（本大题共6小题．共74分，解答给出文字说明，演算步骤）

17．（本小题满分14分）

已知，，，根据下列条件求为钝角三角形的概率：

⑴在线段OB上任取一点C；

⑵过点A任作一直线与直线OB交于点C。

解:(1);　　　　　  (2).

18．（本小题满分14分）

已知抛物线C：y²=4x动直线L：y=k（x+1）与抛物线C交于A、B两点，O为原点

①求证：定值；

②求满足的点M的轨迹方程。

19．（本小题满分14分）

求下列函数的导数：

（1）y=x²sinx；　　　 （2） y=；

解:（1）y′=（x²）′sinx＋x²（sinx）′=2xsinx＋x²cosx.

（2）y′==.

19．（本小题满分14分）用向量法求解下列问题

如图，在直三棱柱ABC—A₁B₁C₁中，AC=BC=AA₁，∠ACB=90°，E、F分别是AB、BC的中点，G是AA₁上的点.

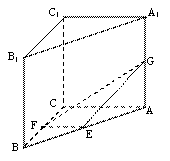⑴如果，试确定点G的位置；

⑵在满足条件（Ⅰ）的情况下，试求的值。

19．解：⑴以C为原点，轴建立空间直角坐标系.

设AC=2，则C（0，0，0），A（0，2，0），C₁（0，0，2）E（1，1，0）　

设　

由即点为的中点。

⑵.　 　　

20. （本小题满分16分）

如图所示，已知A、B、C是长轴长为4的椭圆上的三点，点A是长轴的一个端点，BC过椭圆中心O，且，BC＝2AC．

（I）建立适当的坐标系，求椭圆方程；

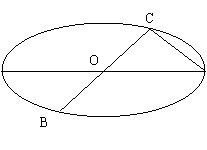（II）如果椭圆上有两点P、Q，使∠PCQ的平分线垂直于AO，证明：存在实数λ，使．

解：（I）以O为原点，OA为X轴建立直角坐标系，设A（2，0），则椭圆方程为

　　　　　∵O为椭圆中心，∴由对称性知OC＝OB

A

　　　　　又∵， ∴AC⊥BC

　　　　　又∵BC＝2AC　　　 ∴OC＝AC

　　　　　∴△AOC为等腰直角三角形　

　　　　　∴点C的坐标为（1，1）　 ∴点B的坐标为（－1，－1）

　　　　　将C的坐标（1，1）代入椭圆方程得，

　　　　　则求得椭圆方程为　　　　　

　　　　　（II）由于∠PCQ的平分线垂直于OA（即垂直于x轴），不妨设PC的斜率为k，则QC的斜率为－k，因此PC、QC的直线方程分别为y＝k（x－1）+1，y＝－k（x－1）+1

　　　　　由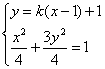　得（1＋3k²）x²－6k（k－1）x＋3k²－6k－1＝0 *）

　　　　　∵点C（1，1）在椭圆上，

　　　　　∴x＝1是方程（*）的一个根，∴x_P•1＝即x_P＝

　　　　　同理x_Q＝　

　　　　　∴直线PQ的斜率为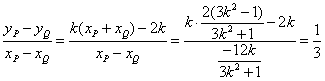（定值）

又∠ACB的平分线也垂直于OA

　　　　　∴直线PQ与AB的斜率相等（∵k_AB=）

　　　　　∴向量，即总存在实数，使成立．

21. （本小题满分16分）

已知椭圆C：＋＝1（a＞b＞0），两个焦点分别为F₁和F₂，斜率为k的直线l过右焦点F₂且与椭圆交于A．B两点，设l与y轴交点为P，线段PF₂的中点恰为B。

（1）若｜k｜≤，求椭圆C的离心率的取值范围；

（2）若k=，A．B到右准线距离之和为，求椭圆C的方程。

解：（1）设右焦点F₂（c，0），则l：y=k（x－c）.令x=0，则y=－ck，∴P（0，－ck）。

∵B为F₂P的中点，∴B（，－）。

∵B在椭圆上，∴＋＝1。

∴k²＝·＝（－1）（4－e²）＝＋e²－5。

∵｜k｜≤，∴＋e²－5≤.∴（5e²－4）（e²－5）≤0。∴≤e²＜1.∴≤e＜1．

（2）k＝，∴e＝.∴＝.

∴a²＝c²，b²＝c².椭圆方程为＋＝1，即x²＋5y²＝c²．

直线l方程为y=（x－c），

B（，－c），右准线为x=c.

设A（x₀，y₀），则（c－x₀）＋（c－）＝，∴x₀＝2c－，y₀＝（c－）.

∵A在椭圆上，∴（2c－）²＋5［（c－）］²＝c².

解之得c=2或c＝（不合题意，舍去）.

∴椭圆方程为x²＋5y²＝5，即＋y²＝1．

第III卷（理科附加题）

（第1、2、3、4题每题6分，第5题16分　共40分）

1．在直角坐标系中，方程所表示的曲线为（　D　）

A．一条直线和一个圆　　　 　B．一条线段和一个圆　　　

C．一条直线和半个圆　　 　　D．一条线段和半个圆

2．双曲线x²－y²＝1的左焦点为F，点P为左支下半支上任意一点（异于顶点），则直线PF的斜率的变化范围是

A．（－∞，0）　　　　　　　　　 B．（1，＋∞）

C．（－∞，0）∪（1，+∞）　　　 D．（－∞，－1）∪（1，＋∞）

解析：数形结合法，与渐近线斜率比较。答案：C

3．已知实数x，y满足3x²+2y²=6x，则x²+y²的最大值是　　 4　 。

4．过双曲线x²－的右焦点作直线交双曲线于A、B两点，且，则这样的直线有

　 3　 条。

5．如图，ADB为半圆,AB为半圆直径,O为半圆圆心，且OD⊥AB，Q为线段OD的中点,已知AB=4，曲线C过Q点，动点P在曲线C上运动，且保持PA+PB的值不变。

　 (1)建立适当的坐标系，求曲线C的方程。

　 (2)过D点的直线L与曲线C相交于不同的两点M,N，求△OMN面积的最大值。

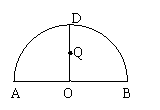　 (3)若过D的直线L与曲线C相交于不同两点M,N,且M在D,N之间,设，求λ的取值范围.

解：以AB、OD所在直线分别为x轴，y轴，O为原点，建立直角坐标系，∵ïAB÷ =4 ∴A(-2,0)　B(2,0),D(0,2) ∴ïPAï+ïPBï=ïQAï+ïQBï=2>ïAB÷ =4

∴曲线C为以O为中心，A,B为焦点的椭圆,设其长半轴为a，短半轴为b，半焦距为c,

则2a=2,2c=4, ∴a= , c=2　, b=1 ∴曲线C方程为

(2)设直线L的方程为y=kx+2,代入曲线C的方程得(1+5k²)x²+20kx+15=0,设M(x­­₁,y₁),N(x₂,y₂)

则 △=(20k)²-4(1+5k²) ·15>0 ①

x­­₁ + x₂=

x­­₁ ·x₂=

由①得k²>3/5

 点O到直线MN的距离d=

弦MN的长ïMNï=ïx­­₁ - x₂ï==

∴S_△OMN =ïMNï·d=··=

设∵k² =∴m>0

则k² =∴S_△OMN=≤=

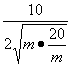当且仅当m=20/m即m=时等号成立，此时k²=∴△OMN的最大面积为

（3）

思路点拨：由得，从而得到M、N的坐标与D点坐标之间的关系：

，代入到椭圆方程中，将可以消去，得到

的关系，利用及，即得。