解析几何综合练习
一、填空题
1.在解析几何的学习中,借助于平面直角坐标系,把曲线插上了方程的“翅膀”,用代数的方法研究图形的性质,使“数”与“形”达到完美的结合,这种方法在数学学习中我们常常叫做_____ _____的思想方法。
2.已知集合![]() ,集合
,集合![]() ,若
,若![]() ,则
,则![]() ____ ____。
____ ____。
3.直线l经过点![]() 且与圆心在原点半径为1的圆面积相切,则直线l的方程是____ ___。
且与圆心在原点半径为1的圆面积相切,则直线l的方程是____ ___。
4.已知定点![]() ,动点
,动点![]() 满足条件
满足条件![]() ,点Q与点P关于直线
,点Q与点P关于直线![]() 对称,则点Q的轨迹是___
___。
对称,则点Q的轨迹是___
___。
5.斜率为2的直线l被曲线![]() 截得的弦长为4,则该弦的中点的坐标是___________________。
截得的弦长为4,则该弦的中点的坐标是___________________。
6.椭圆![]() 的两个焦点为F1、F2,过点F2的直线与椭圆交于A、B两点,则△AF1B的周长是__________。
的两个焦点为F1、F2,过点F2的直线与椭圆交于A、B两点,则△AF1B的周长是__________。
7.以椭圆![]() 的焦点为顶点,顶点为焦点的双曲线方程是___
___。
的焦点为顶点,顶点为焦点的双曲线方程是___
___。
8.双曲线![]() 的一条渐进线与直线
的一条渐进线与直线![]() 垂直,则
垂直,则![]() 。
。
9.双曲线的中心在原点,对称轴是坐标轴,一条渐近线方程为![]() ,且双曲线经过点(2,1),则该双曲线的焦点坐标是____
____。
,且双曲线经过点(2,1),则该双曲线的焦点坐标是____
____。
10.抛物线![]() 的弦
的弦![]() 垂直于
垂直于![]() 轴,若
轴,若![]() 长为4
长为4![]() ,则焦点到
,则焦点到![]() 的距离是________。
的距离是________。
11.若点A的坐标为(3,2),F为抛物线![]() 的焦点,点P是抛物线上的一动点,则
的焦点,点P是抛物线上的一动点,则![]() 取得最小值时点P的坐标是___ ___。
取得最小值时点P的坐标是___ ___。
12.设F1、F2是双曲线![]() 的两个焦点,Q是双曲线上任意一点,从F1引∠F1QF2的平分线的垂线,垂足为P,则点P的轨迹方程是___
____。
的两个焦点,Q是双曲线上任意一点,从F1引∠F1QF2的平分线的垂线,垂足为P,则点P的轨迹方程是___
____。
二、选择题
13.已知集合![]() ,则
,则![]() ( )
( )
(A)![]() (B)M (C)N
(D)以上结论均错
(B)M (C)N
(D)以上结论均错
14.已知椭圆的焦点是F1、F2,点P是椭圆上一动点,如果延长F1P到Q,使得![]() ,那么动点Q的轨迹是( )
,那么动点Q的轨迹是( )
(A)圆 (B)椭圆 (C)双曲线的一支 (D)抛物线
15.双曲线![]() 上一点P,点P到一个焦点的距离为12,则点P到另一个焦点的距离是( )
上一点P,点P到一个焦点的距离为12,则点P到另一个焦点的距离是( )
(A)22或2 (B)7 (C)22 (D)2
16.设坐标原点为O,抛物线![]() 与过焦点的直线交于A、B两点,则
与过焦点的直线交于A、B两点,则![]() ( )
( )
(A)![]() (B)
(B)![]() (C)3
(D)-3
(C)3
(D)-3
三、解答题
17.求下列直线的方程:
(1)直线![]() 绕着它与x轴的交点,按逆时针方向旋转
绕着它与x轴的交点,按逆时针方向旋转![]() 后所得到的直线;
后所得到的直线;
(2)与直线![]() 关于y轴对称的直线。
关于y轴对称的直线。
18.已知圆心在x轴上,半径是5,且以点A (5, 4)为中点,的弦长是![]() ,求这个圆的方程。
,求这个圆的方程。
19.设双曲线![]()
(1)确定实数![]() 的取值范围;
的取值范围;
(2)若点![]() 在双曲线
在双曲线![]() 上,
上,![]() 是两个焦点,
是两个焦点,![]() 与双曲线实轴所在直线垂直,且
与双曲线实轴所在直线垂直,且![]() 的面积为6,求实数
的面积为6,求实数![]() 的值。
的值。
20.过点A (-1, 0)斜率为k的直线l与抛物线![]() 交于P、Q两点,若抛物线C的焦点F与P、Q、R三点构成平行四边形PFQR,求点R的轨迹方程。
交于P、Q两点,若抛物线C的焦点F与P、Q、R三点构成平行四边形PFQR,求点R的轨迹方程。
21.已知曲线C的方程为![]()
(1)若曲线C是椭圆,求k的取值范围;
(2)当k=6时,曲线C上是否存在两点P、Q关于直线![]() 对称。若存在,求出过P、Q的直线方程;若不存在,说明理由。
对称。若存在,求出过P、Q的直线方程;若不存在,说明理由。
22.设![]() 是二次曲线C上的点,且
是二次曲线C上的点,且![]() 构成一个公差为
构成一个公差为![]() 的等差数列,其中O是坐标原点。记
的等差数列,其中O是坐标原点。记![]()
(1)若C的方程为![]() ,点
,点![]() 及
及![]() ,求点
,求点![]() 的坐标;(只需写出一个)
的坐标;(只需写出一个)
(2)若C的方程为![]() ,点
,点![]() ,对于给定的正整数n,
,对于给定的正整数n,
证明:![]() 成等差数列;
成等差数列;
(3)若C的方程为![]() ,点
,点![]() ,对于给定的正整数n,当公差d变化时,求
,对于给定的正整数n,当公差d变化时,求![]() 的最小值。
的最小值。
解析几何综合练习(答案)
一、填空题
1.在解析几何的学习中,借助于平面直角坐标系,把曲线插上了方程的“翅膀”,用代数的方法研究图形的性质,使“数”与“形”达到完美的结合,这种方法在数学学习中我们常常叫做_____数形结合_____的思想方法。
2.已知集合![]() ,集合
,集合![]() ,若
,若![]() ,则
,则![]() ____3或1____。
____3或1____。
3.直线l经过点![]() 且与圆心在原点半径为1的圆面积相切,则直线l的方程是____
且与圆心在原点半径为1的圆面积相切,则直线l的方程是____![]() 或
或![]() ___。
___。
4.已知定点![]() ,动点
,动点![]() 满足条件
满足条件![]() ,点Q与点P关于直线
,点Q与点P关于直线![]() 对称,则点Q的轨迹是___以点
对称,则点Q的轨迹是___以点![]() 为圆心,1为半径的圆___。
为圆心,1为半径的圆___。
5.斜率为2的直线l被曲线![]() 截得的弦长为4,则该弦的中点的坐标是____
截得的弦长为4,则该弦的中点的坐标是____![]() 或
或![]() ____。
____。
6.椭圆![]() 的两个焦点为F1、F2,过点F2的直线与椭圆交于A、B两点,则△AF1B的周长是_____
的两个焦点为F1、F2,过点F2的直线与椭圆交于A、B两点,则△AF1B的周长是_____![]() _____。
_____。
7.以椭圆![]() 的焦点为顶点,顶点为焦点的双曲线方程是___
的焦点为顶点,顶点为焦点的双曲线方程是___![]() ___。
___。
8.双曲线![]() 的一条渐进线与直线
的一条渐进线与直线![]() 垂直,则
垂直,则![]() 。
。
9.双曲线的中心在原点,对称轴是坐标轴,一条渐近线方程为![]() ,且双曲线经过点(2,1),则该双曲线的焦点坐标是____
,且双曲线经过点(2,1),则该双曲线的焦点坐标是____![]() ____。
____。
10.抛物线![]() 的弦
的弦![]() 垂直于
垂直于![]() 轴,若
轴,若![]() 长为4
长为4![]() ,则焦点到
,则焦点到![]() 的距离是______
的距离是______![]() ____。
____。
11.若点A的坐标为(3,2),F为抛物线![]() 的焦点,点P是抛物线上的一动点,则
的焦点,点P是抛物线上的一动点,则![]() 取得最小值时点P的坐标是___(1,2)___。
取得最小值时点P的坐标是___(1,2)___。
12.设F1、F2是双曲线![]() 的两个焦点,Q是双曲线上任意一点,从F1引∠F1QF2的平分线的垂线,垂足为P,则点P的轨迹方程是___
的两个焦点,Q是双曲线上任意一点,从F1引∠F1QF2的平分线的垂线,垂足为P,则点P的轨迹方程是___![]() ____。
____。
二、选择题
13.已知集合![]() ,则
,则![]() ( A )
( A )
(A)![]() (B)M (C)N
(D)以上结论均错
(B)M (C)N
(D)以上结论均错
14.已知椭圆的焦点是F1、F2,点P是椭圆上一动点,如果延长F1P到Q,使得![]() ,那么动点Q的轨迹是( A )
,那么动点Q的轨迹是( A )
(A)圆 (B)椭圆 (C)双曲线的一支 (D)抛物线
15.双曲线![]() 上一点P,点P到一个焦点的距离为12,则点P到另一个焦点的距离是( A
)
上一点P,点P到一个焦点的距离为12,则点P到另一个焦点的距离是( A
)
(A)22或2 (B)7 (C)22 (D)2
16.设坐标原点为O,抛物线![]() 与过焦点的直线交于A、B两点,则
与过焦点的直线交于A、B两点,则![]() ( B )
( B )
(A)![]() (B)
(B)![]() (C)3
(D)-3
(C)3
(D)-3
三、解答题
17.求下列直线的方程:
(1)直线![]() 绕着它与x轴的交点,按逆时针方向旋转
绕着它与x轴的交点,按逆时针方向旋转![]() 后所得到的直线;
后所得到的直线;
(2)与直线![]() 关于y轴对称的直线。
关于y轴对称的直线。
答案:(1)![]() ,(2)
,(2)![]() ;
;
18.已知圆心在x轴上,半径是5,且以点A (5, 4)为中点,的弦长是![]() ,求这个圆的方程。
,求这个圆的方程。
答案:![]() 或
或![]() ;
;
19.设双曲线![]()
(1)确定实数![]() 的取值范围;
的取值范围;
(2)若点![]() 在双曲线
在双曲线![]() 上,
上,![]() 是两个焦点,
是两个焦点,![]() 与双曲线实轴所在直线垂直,且
与双曲线实轴所在直线垂直,且![]() 的面积为6,求实数
的面积为6,求实数![]() 的值。
的值。
解:(1)由题意可得:![]() ,解得
,解得![]() ,
,
则实数![]() 的取值范围是
的取值范围是![]()
(2)由(1)可知双曲线的标准方程为![]() ,
,
则双曲线的两个焦点分别为![]() 、
、![]() ,
,
由题意可设点![]() ,且
,且![]() ,即
,即![]() ,
,
![]() ,
,![]() ,
,![]() ,得
,得![]()
则实数a的值是1.
20.过点A (-1, 0)斜率为k的直线l与抛物线![]() 交于P、Q两点,若抛物线C的焦点F与P、Q、R三点构成平行四边形PFQR,求点R的轨迹方程。
交于P、Q两点,若抛物线C的焦点F与P、Q、R三点构成平行四边形PFQR,求点R的轨迹方程。
解:设直线l的方程为![]() ,代入
,代入![]() 得
得![]() ,设P、Q坐标分别为
,设P、Q坐标分别为![]() 、
、![]() ,R的坐标为
,R的坐标为![]() ,再由
,再由![]() ,得
,得![]() ,
,![]() ,因为线段PQ与RF的中点相同,所以
,因为线段PQ与RF的中点相同,所以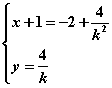 ,消去k,得
,消去k,得![]() ,由
,由![]() ,可得
,可得![]() 。
。
故所求点R的轨迹方程是![]()
21.已知曲线C的方程为![]()
(1)若曲线C是椭圆,求k的取值范围;
(2)当k=6时,曲线C上是否存在两点P、Q关于直线![]() 对称。若存在,求出过P、Q的直线方程;若不存在,说明理由。
对称。若存在,求出过P、Q的直线方程;若不存在,说明理由。
解:(1)k的取值范围是![]() ;
;
(2)当k=6时,曲线方程为![]() ,表示双曲线,若存在两点P、Q关于直线
,表示双曲线,若存在两点P、Q关于直线![]() 对称。设直线PQ的方程为
对称。设直线PQ的方程为![]() ,由
,由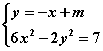 得
得![]() ,设线段PQ的中点为
,设线段PQ的中点为![]() ,则
,则![]() ;又点M在直线
;又点M在直线![]() 上,所以
上,所以![]() ,可验证此时
,可验证此时![]() 因此,存在满足题设条件的两点P、Q,直线PQ的方程是
因此,存在满足题设条件的两点P、Q,直线PQ的方程是![]()
22.设![]() 是二次曲线C上的点,且
是二次曲线C上的点,且![]() 构成一个公差为
构成一个公差为![]() 的等差数列,其中O是坐标原点。记
的等差数列,其中O是坐标原点。记![]()
(1)若C的方程为![]() ,点
,点![]() 及
及![]() ,求点
,求点![]() 的坐标;(只需写出一个)
的坐标;(只需写出一个)
(2)若C的方程为![]() ,点
,点![]() ,对于给定的正整数n,
,对于给定的正整数n,
证明:![]() 成等差数列;
成等差数列;
(3)若C的方程为![]() ,点
,点![]() ,对于给定的正整数n,当公差d变化时,求
,对于给定的正整数n,当公差d变化时,求![]() 的最小值。
的最小值。
解:(1)可解得P3的坐标为![]() ;
;
(2)若![]() ,则
,则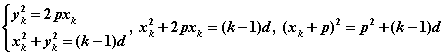 ,
,
所以![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列。
的等差数列。
(3)原点O到曲线C上各点的最小距离为b,最大距离为a.
![]() ,且
,且![]() ,
,![]()
![]() 在
在![]() 上单调递增,故
上单调递增,故![]() 的最小值为
的最小值为![]() ,即为
,即为![]()