高二数学第一学期期中考试
试卷
平潭私立城东中学
（完卷时间120分钟，满分150分）
一、单项选择题（每题5分，共55分）
1． 若a＜0，—1＜b＜0,则a.、ab、ab
的大小关系是（ ）
A．ab＞ ab＞a B．
a＞ab＞ab C．ab＞
ab＞a D．ab＞a＞ ab
2．已知：a>1,则a+ 
的最小值为（ ）
A． 2 B． 3 Ｃ ． －
Ｄ． ２
3．下列不等式中与 x＜３ 同解的是（ ）
A．x+
＜３＋ B．x
＜
C．x +
＜3+
D．x
＜3
4．若不等式： 
＜2 与 
＞
同时成立，则 x 的取值范围是（ ）
A．（－
，） B．(，+
)
（－，－）
C．(，+)（－，） D．(，+)
5．若不等式（x＋a）(x+4 x+3) ≥0的解为[－３，－１][2，+ )，则a的值为（ ）
Ａ．２ Ｂ．－２ Ｃ．－１ Ｄ．－３
6．已知直线 m x +4y－2=0 与直线 2 x－5 y ＋n=0 垂直，垂足为 （１，p） ，则m、n、p的值分别是（ ）
A．m=10 p=2 n=－12 B．m=10 p=－2 n=－12
C．m=－10 p=－2 n=－12 D．m=－
p=－2 n=－12
7．直线a x
+b y +c=0的倾斜角为
，且sina+cos=0，则a、b满足（ ）
A．a＋b=1 B．a＋b=0 C．a－b=0 D．a－b=1
8．将一张坐标纸折叠一次，使得点（0，2）与点（—2，0）重合，且点（2005，2006）与点（m，n）重合，则m－n 的值为（ ）
A．－1 B．1 C．0 D．2
9．由不等式≤
≤
及≤２围成的平面区域的面积为（ ）
A．2 B．3 C．4 D．
10．已知BC是圆
上的动弦，若
，则弦BC的中点轨迹方程为（ ）
A．
B．
C．
D．
11．已知一圆过点A（4，—2）且过两直线
：
，
：
的交点，且在y轴上截得的线段长为
；则所求的圆的方程为（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
二、填空题：（每题5分，共30分）
12．设
（0，2），则
= 时，函数
的最大值为 。
13．已知两直线：
， ：
，当这两条直线的夹角在（0， 
）内变动时，a的取值范围是 。
14．过圆
外一点p(2,3)的圆的切线方程为 。
15．若点（
）在圆
上运动，则动点（
）的轨迹方程为
（化为普通方程）
16．已知两直线：
，：
，若直线平行直线，并且坐标原点到、 的距离相等，则a、b 的值为 。
17．给出以下命题：
①经过任意两个不同点
、
的直线都可以用方
来表示；
②过点
且在、 轴上截距相等的直线方程是：
；
③若
且
，则
≥２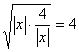
；
④若直线
不通过第二象限，则
的值的取值范围是：＜
，
其中正确命题的序号是 。
三、解答题：（每大题13分）
18．证明下列不等式：
（1）设
且
求证：
＜
（2）已知＞０，
＞０，求证：
≥
19．解不等式：
≤ 
20．某咖啡店需配制甲、乙两种饮料，每种饮料所需原料及获利情况如下表所示：
| 原料 种类 | 奶粉 | 咖啡 | 糖 | 获利
|
| 甲 （杯） | 9 | 4 | 3 | 0.7 |
| 乙 （杯） | 4 | 5 | 10 | 1.2 |
又知每天原料使用限量为：奶粉3600
，咖啡2000，糖3000，若每天在原料使用限量内,饮料能全部售出，问：每天应配制甲、乙饮料各多少杯，才能使获利最大？最大获利是多少？
21．过平面上一点
引直线
，使它在两坐标轴上的截距都为正，且它们的和最小，求直线的方程。