高二数学第一学期期中考试试卷2
第I卷（命题人：盛燕华）
（考试时间:120＋30分钟 总分:160分+40分）
一、选择题（共12题，每小题5分，共60分）
1．
抛物线
的焦点坐标是
A．
B。
C。 
D。
2．下列求导正确的是
A． 
B．
C．
D．
3．双曲线
的离心率
，则k的取值范围为
A．
B。
C。
D。
4．已知圆C：
，点A
及点B（3，a），从A点观察B点，要使视线不被圆C：挡住，则实数a的取值范围是
A
B
C
D
5．椭圆短轴长是2，长轴是短轴的2倍，则椭圆中心到其准线的距离是
A．
B 。
C。
D。
6．设
是
椭圆的焦点，点P是椭圆上的点，若
，则这样的点P有
A．2个 B。0个 C。3个 D。4个
7．已知
，则
=
A．0 B。
C。 
D。2
8． 已知点P为抛物线
上的动点，M是抛物线的焦点，点A的坐标为
，则PA+PM的最小值
A．
B。
D。5
9．已知曲线
在点Ｍ处的瞬时变化率为－４，则点Ｍ的坐标是
Ａ。（１，３） Ｂ。（４，３３） Ｃ。（－１，３） Ｄ。不确定
10．设双曲线Ｃ：
的右焦点为Ｆ，直线ｌ过点F且斜率为ｋ，若直线ｌ与双曲线Ｃ的左右两支都相交，则直线ｌ的斜率的取值范围
Ａ。
Ｂ。
Ｃ。
Ｄ。
11．设
，
，
……，
，
，则
Ａ。
Ｂ。
Ｃ。
Ｄ。
１2。过双曲线
的右焦点Ｆ作直线ｌ交双曲线于Ａ，Ｂ两点，若ＡＢ＝３，则这样的直线共有
Ａ。１条 Ｂ。２条 Ｃ。３条 Ｄ。４条
2006~2007学年度第一学期期中考试试卷
高二数学
第II卷（命题人：盛燕华）
| 结分人 | 核分人 | 总分 |
| 得分 | 阅卷人 |
二．填空题（共６题，每题５分，共３０分）
13．函数
的导数_______________________________
14．一抛物线型拱桥，当桥顶离水面
_________________________________
15．已知
，则
_____________________________
16．已知斜率为1的直线过椭圆的
右焦点交椭圆于A，B两点，求弦AB的长
____________________________
17．求与双曲线
有公共渐近线且焦距为8的双曲线方程__________________
18．若
，求
________________________
三．解答题（共5题，共70分）
| 得分 | 阅卷人 |
19．（14分）抛物线顶点在原点，它的准线过双曲线
的一个焦点并与双曲线实轴垂直，已知抛物线与双曲线的交点为
，求抛物线和双曲线的方程
| 得分 | 阅卷人 |
20．（14分）已知直线l与曲线
相切，分别求满足下列条件l的方程
（1）l经过点
（2）l经过点（2， 0）
（3）l平行于直线
| 得分 | 阅卷人 |
21．（14分）设椭圆
的左焦点为
，左准线
与x轴交于点N（-3，0），过点N且倾斜角为
的直线l交椭圆于A，B两点
（1）求直线l和椭圆的方程
（2）求证：点
在以线段AB为直径的圆上
| 得分 | 阅卷人 |
22．（12分）如图，身高1。
（1）求身影的长度y与人距路灯的距离x之间的关系；
（2）解释身影长的变化率与人步行速度的关系；
（3）求x=
| 得分 | 阅卷人 |
23．（16）已知：某椭圆的焦点是
过点
并垂直与x轴的直线与椭圆的一个交点为B，且
，椭圆上不同的两点
满足条件：
成等差数列。
（1）求该椭圆的方程；
（2）求弦AC中点的横坐标
（3）设AC的垂直平分线的方程为y=kx+m，求m的取值范围
| 得分
| 阅卷人 |
附加题（共40分）（1—7班做）
1． 5（分）下列函数中，在x=0处的导数不等于0的是
A．
B。 y=x（1-x） C。
D。
2．5（分）双曲线的一个焦点固定，它的两条分支各过一个定点，则另一个焦点的轨迹
是
A．双曲线 B。 椭圆 C。抛物线 D。两条相交直线
3．（5分）点M与点F（3，0）的距离比它到直线x+5=0的距离小2，则点M的轨迹方程为————————
4．（5）分过椭圆
内一点M（2，0）引椭圆的动弦AB，则弦AB的中点N的轨迹方程是————
）
5．（5分）若质点的运动方程是
，则质点在t=3时的瞬时速度为——————————————
6（15）已知，
，试讨论方程
所表示的曲线方程
答案
选择题
1~5 CDCAD 6~10DBDCC 11~12DB
填空题
13.sinx+xcosx 14.
15.-2 16.
17.
18.
19~23解答题
19.抛物线方程
双曲线方程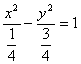
20.
21.直线方程
椭圆方程
证明题略
22.(1)
(2)人影长的变化率等于人步行的0.75倍
(3)
23.(1)
(2)4
(3)
附加题
1.B2.B
3.
4.
5.sin6+6cos6
6.略