高二数学第一学期月考试卷
总分100分
第 I 卷 (选择题 共50分)
一、 选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
1.
若 ![]() , 则下列正确的是
, 则下列正确的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.
在△ABC中,若a = 2 ,![]() ,
,![]() , 则B等于
, 则B等于
A.![]() B.
B.![]() 或
或 ![]() C.
C.![]() D.
D.![]() 或
或![]()
3.
如果数列![]() 是等差数列,则
是等差数列,则
A.![]() =
=![]() B.
B.![]() <
<![]()
C.![]() >
> ![]() D.
D.![]() =
=![]()
4.
不等式![]() 的解集为
的解集为
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
5. 在⊿ABC中,已知![]() ,则C=
,则C=
A .300
B.
6. 已知:在⊿ABC中,![]() ,则此三角形为
,则此三角形为
A. 直角三角形 B. 等腰直角三角形
C. 等腰三角形 D. 等腰或直角三角形
7.
若不等式![]() 的解集
的解集![]() 则a-b值是
则a-b值是
A.-10 B.-
8.
观察下面的数阵,容易看出,第n+1行最右边一个数与第n行最右边一个数满足![]() ,则前20行的所有数字之和为
,则前20行的所有数字之和为
1
2 3
4 5 6
7 8 9 10
11 12 13 14 15
… … … … … …
A.22155 B
9.
两个等差数列![]() 和
和![]() ,其前
,其前![]() 项和分别为
项和分别为![]() ,且
,且![]() 则
则![]() 等于
等于
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
10.
若关于![]() 的不等式
的不等式![]() 内有解,则实数
内有解,则实数![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第 Ⅱ 卷 (非选择题 共100分)
二.填空题:(本大题共6小题;每小题5分,共30分.)
11.
若![]() ,
,![]() ,则a-b的取值范围是
.
,则a-b的取值范围是
.
12. 在△ABC中,BC=2,AC=2,C=1500,则△ABC的面积为 .
13. 设{an}是各项均为正数的等比数列,前4项之和等于其前2项和的10倍,则该数列的公比为____ __.
14. 设![]() 满足约束条件:
满足约束条件: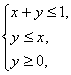 则
则![]() 的最大值是 .
的最大值是 .
15.
![]() .
.
16. 已知奇函数f(x)在(0,+∞)内单调递增,且f(2)=0,则不等式(x-1)·f(x)<0的解集是 .
三.解答题:(本大题共小题,共分.解答应写出文字说明、证明过程或推证过程.)
17. 求不等式组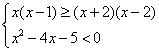 的解集。
的解集。
18.
设数列![]() 的前n项和为
的前n项和为![]() ,点
,点![]() 均在函数y=-x+12的图像上.
均在函数y=-x+12的图像上.
(Ⅰ)写出![]() 关于n的函数表达式;
关于n的函数表达式;
(Ⅱ)求证:数列![]() 是等差数列.
是等差数列.
19. 在⊿ABC中,三个角A、B、C的大小成等差数列,若此三角形的周长为20,面积为![]() .求三边长.
.求三边长.
20. 某厂用甲、乙两种原料生产A、B两种产品,已知生产1t A产品,1t B产品分别需要的甲、乙原料数,可获得的利润数及该厂现有原料数如下表所示.问:在现有原料下,A、B产品应各生产多少才能使利润总额最大?列产品和原料关系表如下:
|
| A产品 (1t) | B产品 (1t) | 总原料 (t) | ||
| 甲原料(t) | 2 | 5 | 10 | ||
| 乙原料(t) | 6 | 3 | 18 | ||
| 利润(万元) | 4 | 3 |
21.
设关于x的一元二次方程![]() (
(![]() )有两根
)有两根![]() 和
和![]() ,且满足
,且满足![]() .
.
(1)试用![]() 表示
表示![]() ;
;
(2)求证:数列{![]() }是等比数列;
}是等比数列;
(3)当![]() 时,求数列{
时,求数列{![]() }的通项公式.
}的通项公式.
答案:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D
| B | A | A | C | C | A | A | D | A |
11.![]() 12. 1
13. 3
14. 2
12. 1
13. 3
14. 2
15.![]() 16.
16.![]()
17.![]()
18.(1)![]() (2)略
(2)略
19.![]() 或
或![]()
20.A:![]() B:
B:![]()
21.(1)![]()
(2)略
(3)![]()