高二数学椭圆测试题(一)
一.选择题(每小题5分,满分30分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若直线![]() 和椭圆
和椭圆![]() 相切, 则
相切, 则![]() 的值是………………………[ C ]
的值是………………………[ C ]
A.1 / 2 B.2
/
![]()
![]() 2.椭圆
2.椭圆![]() 与直线x+y-1=0交于M、N两点,过原点与线段MN中点的直线斜率为
与直线x+y-1=0交于M、N两点,过原点与线段MN中点的直线斜率为
,则 的值是…………………………………………………………………[ B ]
A. B. C. D.
3.椭圆![]() 上对两焦点张角为
上对两焦点张角为![]() 的点可能有………………………………[ C ]
的点可能有………………………………[ C ]
![]() 4.
4.![]() 是椭圆短轴的两端点,过左焦点
是椭圆短轴的两端点,过左焦点![]() 作长轴的垂线,交椭圆于P,若
作长轴的垂线,交椭圆于P,若![]() 是
是![]() 和
和![]() 的比例中项,则
的比例中项,则![]() :
:![]() 的值是……………………………………………[ B ]
的值是……………………………………………[ B ]
5.椭圆![]() 的一个焦点为
的一个焦点为![]() ,点P在椭圆上,如果线段
,点P在椭圆上,如果线段![]() 的中点M在y轴上,那么点M的纵坐标是…………………………………………………………………………[ A ]
的中点M在y轴上,那么点M的纵坐标是…………………………………………………………………………[ A ]
A. B. C. D.
6.设A(-2,![]() ),F为椭圆
),F为椭圆![]() =1的右焦点,点M在椭圆上移动,当AM+2MF取最小值时,点M的坐标为…………………………………………………………………[ C ]
=1的右焦点,点M在椭圆上移动,当AM+2MF取最小值时,点M的坐标为…………………………………………………………………[ C ]
A.(0,2![]() ) B.(0,-2
) B.(0,-2![]() ) C.(2
) C.(2![]() ,
,![]() ) D.(-2
) D.(-2![]() ,
,![]() )
)
二.填空题(每题5分,满分20分,把答案填在题中横线上)
 7.椭圆
7.椭圆![]() =1上有一点P到左准线的距离为2.5,则P到右焦点的距离为 .
=1上有一点P到左准线的距离为2.5,则P到右焦点的距离为 .
8.
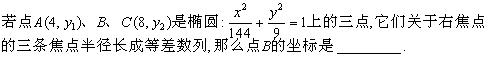 9.
9.
10.P是椭圆![]() =1上的点,F1和F2是焦点,则k=PF1·PF2的最大值和最小值分别是________
=1上的点,F1和F2是焦点,则k=PF1·PF2的最大值和最小值分别是________
1.8 2.1/2 3.![]() 4.kmax=4,kmix=3
4.kmax=4,kmix=3
三.解答题(11,12题每题15分,13题20分,满分50分,解答应写出文字说明,证明过程或演算步骤)
11. 已知椭圆的焦点在坐标轴上,短轴的一个端点与两焦点构成正三角形,若焦点到椭圆的最短距离为![]() ,求椭圆的标准方程.
,求椭圆的标准方程.
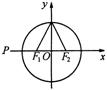 解:如图所示,设点P(
解:如图所示,设点P(![]() ,
,![]() )为椭圆上位于第一象限的任一点,其到焦点距离
)为椭圆上位于第一象限的任一点,其到焦点距离![]() ,显然
,显然![]() 时,
时,![]() 最小,故有
最小,故有![]() ,由短轴端点与两焦点构成正三角形得
,由短轴端点与两焦点构成正三角形得![]() ,a=
,a=![]() ,b=3.
,b=3.
故![]() 与
与![]() 为所求椭圆方程.
为所求椭圆方程.
12. 设中心在原点,焦点在x轴上的椭圆的离心率为![]() ,并且椭圆与圆x2+y2-4x-2y+
,并且椭圆与圆x2+y2-4x-2y+![]() =0交于A、B两点,若线段AB的长等于圆的直径.
=0交于A、B两点,若线段AB的长等于圆的直径.
(1)求直线AB的方程;
(2)求椭圆的方程.
解:(1)设椭圆的方程为![]() ,由
,由![]() 及
及![]() 得
得![]() ,
,
设![]() ,由于线段AB的长等于圆的直径,所以线段AB的中点为圆心(2,1),且
,由于线段AB的长等于圆的直径,所以线段AB的中点为圆心(2,1),且![]() ,则
,则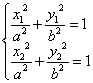 ,两式相减得
,两式相减得
![]() ,
,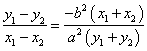 ,又
,又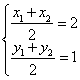 ,所以
,所以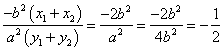 ,
,![]() ,直线AB的方程为y=-
,直线AB的方程为y=-![]() x+2;
x+2;
(2)由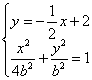 ,消去x得
,消去x得![]() ,
,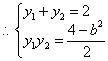 ,
,
![]() ,又
,又![]() ,所以
,所以![]() ,
,
![]() ,又
,又![]() ,
,![]() ,
,
![]() ,所求椭圆的方程为
,所求椭圆的方程为![]() +
+![]() =1.
=1.
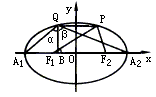
13.设椭圆![]() +
+![]() =1的两焦点为F1、F2,长轴两端点为A1、A2.
=1的两焦点为F1、F2,长轴两端点为A1、A2.
(1)P是椭圆上一点,且∠F1PF2=600,求ΔF1PF2的面积;
(2)若椭圆上存在一点Q,使∠A1QA2=1200,求椭圆离心率e的取值范围.
解:(1)设PF1=r1,PF2=r2,则S![]() =
=![]() r1r2sin∠F1PF2,由r1+r2=
r1r2sin∠F1PF2,由r1+r2=
![]() .代入面积公式,得
.代入面积公式,得
S![]() =
=![]() b2=b2tan∠
b2=b2tan∠![]() =
=![]() b2.
b2.
(2)设∠A1QB=α,∠A2QB=β,点Q(x0,y0)(0<y0<b).![]() =tan(α+β)=
=tan(α+β)= ![]() =
= 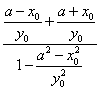 =
=![]() .∵
.∵![]() +
+![]() =1,∴x02=a2-
=1,∴x02=a2-![]() y02.
y02.
 ∴tanθ=
∴tanθ=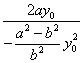 =
=![]() =-
=-![]() .∴2ab2=
.∴2ab2=![]() c2y0≤
c2y0≤![]() c2b, 即
c2b, 即
∴3e4+4e2-4≥0,解之得e2≥![]() ,∴
,∴![]() ≤e<1为所求.
≤e<1为所求.