高二数学下学期期中考试
试卷
一、选择题（每小题3分，共45分）
1、过点
与已知直线
垂直的直线方程为
A、
B、
C、
D、
2、直线
两两平行，经过其中2条直线的平面共有
A、3个 B、1个 C、1个或3个 D、4个
3、设
分别是长方体的相对两个面的对角线所在直线，则
与
（）
A、平行 B、相交 C、异面或相交 D、平行或异面
4、
中，
平面
，
，则
到
的距离是
A、
B、
C、
D、
5、直线与平面
所成的角为
，直线
，直线与直线所成的角为
，则有
A、
B、
C、
D、
6、已知实数
满足
则
的最小值为
A、
B、
C、9
D、7
7、过点
，圆心在直线
上的圆的方程为
A、
B、
C、
D、
8、已知
，则以它们为顶点的四边形为
A、平行四边形 B、梯形 C、菱形 D、正方形
9、椭圆
的焦点坐标为
A、
B、
C、
D、
10、曲线
关于直线
对称的曲线方程是
A、
B、
C、
D、
11、椭圆
上一点P到两焦点的距离之和与该点到两准线的距离之和的比是
A、
B、
C、
D、随P的位置不同而变化
12、若椭圆
与双曲线
的焦点相同，则
的值为
A、11
B、
13、抛物线
的焦点纵坐标与它的通径的比是
A、4
B、
C、
D、
14、中心在原点，对称轴是两坐标轴，有一条渐近线为
，且过点
的双曲线方程是
A、
B、
C、
D、
15、在棱长为1的正方体
中，
分别为棱
的中点，点
是正方形
中心，则空间四边形
在正方体六个面内的射影所构成的图形中最大面积为
|
B、
C、
D、1
二、填空题（每小题3分，共15分）
16、已知
，则
到
的角大小为
17、双曲线
上一点P到一个焦点的距离等于1，则P到另一个焦点的距离等于
18、P为所在平面外一点，O为P在平面ABC上的射影，若
，
则O是的
心（填外心、内心、垂心、中心之一）
19、已知平面和直线
，以下四个命题中
①
，则
②若
则
③
则
与相交
④若与所成的角相等，则
正确的命题是
20、两圆
及
，在它们的交点处切线互相垂直，则
=
数学答题卷
|
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题： （每小题3分，共15分）
16、 17、 18、 19、 20、
三、解答题
21、的顶点是
（1）求BC边上中线所在直线方程
（2）求BC边上高线所在直线方程（8分）
22、从圆C：
外一点P（2，3）向这个圆引两切线PA、PB
（1）求两切线方程
（2）求四边形PACB的面积（8分）
23、一个圆经过点F（2，0），且和直线x+2=0相切
（1）求圆心的轨迹方程
（2）在（1）中轨迹上求一点M，使它到定点A（3，0）的距离最小，并求出这个最小值（8分）
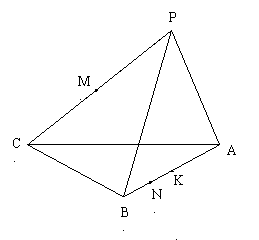
24、如图，是所在平面外一点，
，
是
的中点，
是
上的点，
，
是中点
（1）求证：
（2）当
时，求
的长（8分）
 |
25、已知
是椭圆
的左右焦点，
是椭圆上位于第一象限内的一点，点
也在椭圆上，且满足
（
为坐标原点），
，若椭圆的离心率
（1）求直线的方程
（2）若
的面积为
，求椭圆方程（8分）
参考答案
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 答案 | D | C | D | D | B | C | A | D | C | D | B | C | D | C | B |
二、填空题:
16、
17、17 18、垂心 19、①③ 20、3
三、解答题:
21、（1）
（4分）（2）
（8分）
22、（1）
（4分） （2）2（8分）
23、（1）
（4分） （2）3（8分）
24、（1）略（4分） （2）
（8分）
25、（1）
（4分） （2）
（8分）