高二上学期期中考试数学文科试卷
总分150分
一、选择题：本大题共10小题；每小题5分，共50分，在每小题给出的四个选项中，只有一个选项是符合题目要求的。
1．在△ABC中，若a = 2 ,
,
, 则B等于( )
A．
B．或 
C．
D．或
2．若命题p：2n－1是奇数，q：2n＋1是偶数，则下列说法中正确的是 （ ）
A．p或q为真 B．p且q为真 C． 非p为真 D． 非q为假
3．如图，为了测量隧道两口之间AB的长度，对给出的四组数据，计算时要求最简便，测量时要求最容易，应当采用的一组是
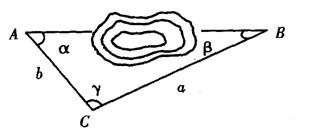
A．
B．
C．
D． 
4、已知函数
的定义域为A,函数
的定义域为B, 则A
B=( )
A 、x>5
B、
C、
D、
5．若椭圆的两焦点为（－2，0）和（2，0），且椭圆过点
，则椭圆方程是 （ ）
A．
B．
C．
D．
6．
＞1的一个充分不必要条件是 ( )
A．x＞y B．x＞y＞
7．已知数列
的前n项和
，则( )
A．
=
B．=
C．=
D．=
8、已知椭圆
与椭圆
有相同的短轴，椭圆的长轴长与椭圆
长轴长相等，则（ ）
A、
16，
21
B、21， 9
C、21，16或16，21
D、21， 16
9、下列方程中，以x±2y=0为渐近线的双曲线方程是
(A)
10．过点M（－2，0）的直线m与椭圆
交于P1，P2，线段P1P2的中点为P，设直线m的斜率为k1（
），直线OP的斜率为k2，则k1k2的值为 （ ）
A．2 B．－
D．－
二、填空题：本大题共4题；每小题5分，共20分，把答案填在题中的横线上。
11、写出下列命题的否定形式。
①有理数是实数；_____________________________.
②有些平行四边形不是菱形；_________________________________.
③"x∈R，x2-2x>0；________________________________.
12．1与 
的等比中项是
13、椭圆
与双曲线
的焦点相同，则a=____________
14．已知椭圆Ｅ的短轴长为6，焦点Ｆ到长轴的一个端点的距离等于９，则椭圆Ｅ的离心率等于__________________．
三。、解答题：本大题共6小题，共80分，解答应写出必要的文字说明、证明过程及演算步骤。
15．（本小题12分）写出原命题“若
，则
”的逆命题、否命题、逆否命题，再判断这四个命题的真假．
16．（本小题14分）已知是等差数列，其中
（1）求数列的通项公式。
（2）求
值。
17、（本小题12分）双曲线的离心率等于
，且与椭圆
有公共焦点，求此双曲线的方程。
18．（本小题14分）某家公司每月生产两种布料A和B，所有原料是三种不同颜色的羊毛，下表给出了生产每匹每种布料所需的羊毛量，以及可供使用的每种颜色的羊毛的总量。
| 羊毛颜色 | 每匹需要 / kg | 供应量/ kg | |
| 布料A | 布料B | ||
| 红 | 4 | 4 | 1400 |
| 绿 | 6 | 3 | 1800 |
| 黄 | 2 | 6 | 1800 |
已知生产每匹布料A、B的利润分别为120元、80元。那么如何安排生产才能够产生最大的利润？最大的利润是多少？
19、（本小题14分）已知点M到定点A(0,-2
)与到定直线
的距离之比等于,求点M的轨迹.并说明轨迹的形状是什么。
20、（本小题14分）已知椭圆
及直线
，若该直线被椭圆截得的弦长为
，求该直线的方程。
测试题答题卡
选择题(50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
填空题(20分)
11①___________________________.②_____________________________
③_____________________________. 12____________
13__________ 14____________
三、解答题
15、解：
16、解：
17、解：
18、解：
19解：
20、解：
高二数学文科试卷答案
一、选择题
1、B 2、A 3、A 4、C 5、D 6、B 7、C 8、D 9、A 10、D
二、填空题
11、①存在一些有理数不是实数. ②所有平行四边形是菱形.
③
12、
13、1 14、
三、解答题
15、解：逆命题：若，则。 …………………………3分
否命题：若
，则
。
……………………6分
逆否命题：若，则。…………………………9分
其中原命题与逆否命题是真命题，逆命题与否命题是假命题。 ………………………12分
16、解：（1）
………………………2分
………………………4分
………………………5分
=25+
………………………7分
（2）
………………………10分
=
………………………14分
17、解：椭圆的焦点为
焦点在
轴上。
………………4分
在双曲线中，
………………6分
又
………………8分
………………10分
双曲线的方程为 
………………12分
18. 解：设每月生产布料A、B分别为x匹、y匹，利润为Z元，那么
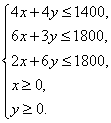①
………………………………2分
目标函数为 
………………………………4分
作出二元一次不等式①所表示的平面区域（阴影部分）即可行域。
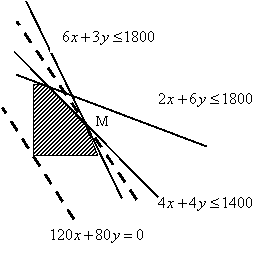
………………………………………8分
把变形为
，得到斜率为
，在轴上的截距为
，随z变化的一族平行直线。如图可以看出，当直线经过可行域上
M时，截距最大，即z最大。 …………………………10分
解方程组
得M的坐标为x=250 , y=100 ……………………………12分
所以
……………………………13分
答：该公司每月生产布料A、B分别为250 、100匹时，能够产生最大的利润，最大的利润是38000 元。 ……………………………………………14分
19、解：设点M的坐标为
，点M到定直线的距离为
根据题意有：
……………………4分
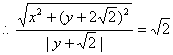……………………6分
上式两边平方，化简得
……………………12分
它是焦点在
轴上的等轴双曲线。
……………………14分
20、解：设直线被椭圆截得两点坐标分别为
则
① ……………………2分
，
……………………4分
①式化为
……………………6分
=
，
②
……………………8分
联立方程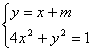
消元化简得
……………………10分
代入②式，得
……………………12分
所求直线的方程为
。
……………………14分