高二数学(文)八校联考试题
一、选择题(每小题5分,共10题,50分)
1、设![]() 是集合A到集合B的映射,若
是集合A到集合B的映射,若![]() ,则
,则![]() 为……………( )
为……………( )
A、![]() B、
B、![]() C、
C、![]() 或
或![]() D、
D、![]() 或
或![]()
2、![]() :如果
:如果![]() 那么
那么![]()
![]() :
:![]() 那么
那么![]() 是
是![]() 的( )条件………………………………………………( )
的( )条件………………………………………………( )
A、充分不必要 B、必要不充分 C、充要 D、既不充分也不必要
3、函数![]() 在区间
在区间![]() 上存在反函数,则
上存在反函数,则![]() 的取值范围是……………( )
的取值范围是……………( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、已知复数![]() ,则
,则![]() 的值是…………………………………( )
的值是…………………………………( )
A、1
B、![]() C、
C、![]() D、
D、![]()
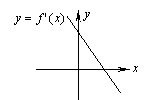 5、函数
5、函数![]() 的图象过原点且它的导函数
的图象过原点且它的导函数![]() 的图象是如图所示的一条直线,
的图象是如图所示的一条直线,![]() 的图象的顶点在…………………………………………………………( )
的图象的顶点在…………………………………………………………( )
A、第Ⅰ象限
B、第Ⅱ象限
C、第Ⅲ象限
D、第Ⅳ象限
6、设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,当
,当![]() 变化时,
变化时,
若![]() 是一个定值,那么下列各项中也为定值的是
是一个定值,那么下列各项中也为定值的是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7、![]() 展开式中的常数项为……………………………………………………( )
展开式中的常数项为……………………………………………………( )
A、![]() B、
B、![]()
8、从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法共有……………………………………………………………( )
A、14
B、
9、已知奇函数![]() 在
在![]() 上为减函数,且
上为减函数,且![]() ,则不等式
,则不等式![]() 的解集为 …………………………………………………………………………………( )
的解集为 …………………………………………………………………………………( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
10、已知数列![]() 前
前![]() 项和为
项和为![]() ,则
,则![]() 的值是…………………………………………………………………………………( )
的值是…………………………………………………………………………………( )
A、13
B、![]() C、46
D、76
C、46
D、76
二、填空题(每小题4分,共7题,28分)
11、以![]() 为切点,曲线
为切点,曲线![]() 的切线的倾斜角为___________.
的切线的倾斜角为___________.
12、数学![]() 对任意
对任意![]() 都满足
都满足![]() 且
且![]() ,
,![]() ,
,![]() ,则
,则![]() _____.
_____.
13、甲射击命中目标的概率是![]() ,乙射击命中目标的概率是
,乙射击命中目标的概率是![]() ,丙射击命中目标的概率是
,丙射击命中目标的概率是![]() ,现在三人同时射击目标,则目标被击中的概率为________.
,现在三人同时射击目标,则目标被击中的概率为________.
|
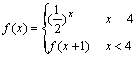 ,则
,则15、奇函数![]() 在
在![]() 处有极值,则
处有极值,则![]() 的值为__________.
的值为__________.
16、一圆形餐桌依次有A、B、C、D、E、F共6个座位,现让3个大人和3个小孩入座进餐,要求任何两个小孩都不能坐在一起,则不同的入座方法总数为______________.
17、设集合![]() ,
,![]() 且
且![]() ,则实数
,则实数![]() 的取值范围是_________________.
的取值范围是_________________.
三、解答题(第18—21题每小题14分,第22题16分,共72分)
18、设数列![]() 是等差数列,
是等差数列,![]() 是首项为1的等比数列,
是首项为1的等比数列,![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
19、设函数![]() ,不等式
,不等式![]() 的解集为
的解集为![]()
(Ⅰ)判断![]() 的单调性,并用定义证明;
的单调性,并用定义证明;
(Ⅱ)解不等式![]() .
.
20、某人有5把钥匙,一把是房门钥匙,但忘记了开房门的是哪一把。于是,他逐把不重复地试开,问:
⑴恰好第三次打开房门锁的概率是多少?
⑵三次内打开的概率是多少?
⑶如果5把内有2把房门钥匙,那么三次内打开的概率是多少?
21、设函数![]()
(Ⅰ)求函数![]() 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若当![]() 时,恒有
时,恒有![]() ≤
≤![]()
![]() ,试确定
,试确定![]() 的取值范围.
的取值范围.
22、已知函数![]() 的图象过点
的图象过点![]() ,且方程
,且方程![]() 有两个相等的实数根.
有两个相等的实数根.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)若正项数列![]() 满足:
满足:![]() ,求通项
,求通项![]() ;
;
(Ⅲ)对满足(Ⅱ)中的数列![]() ,若数列
,若数列![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,证明
项和,证明![]() .
.
高二数学(文)八校联考试题答题卷
一、选择题(每小题5分,共10题,50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题(每小题4分,共7题,28分)
11、__________________ 12、__________________ 13、__________________
14、__________________ 15、__________________ 16、__________________
17、__________________
三、解答题(第18—21题每小题14分,第22题16分,共72分)
18、
19、
20、
21、
22、
高二数学(文)八校联考答案
一、选择题(每小题5分,共10题,50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | A | D | A | A | C | B | B | C | B |
二、填空题(每小题4分,共7题,28分)
11、![]() 12、8 13、
12、8 13、![]() 14、
14、![]() 15、0 16、72 17、
15、0 16、72 17、![]() ≤
≤![]() ≤1
≤1
三、解答题(第18—21题每小题14分,第22题16分,共72分)
18、∵![]() ,∴
,∴![]() ,
2分
,
2分
设数列{![]() }的公差为
}的公差为![]() ,数列{
,数列{![]() }的公比为
}的公比为![]() ,则
,则 ![]()
解得![]() 或
或![]() 12分
12分
所以数列{![]() }的通项公式为
}的通项公式为![]() 14分
14分
19、(Ⅰ)解:∵![]() <
<![]() 得
得![]() <
<![]() <
<![]()
又∵![]() <
<![]() 的解集为
的解集为![]()
∴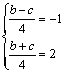 得
得![]() 4分
4分
函数![]() 在
在![]() 上为增函数
6分
上为增函数
6分
证明:设![]() >
>![]() >
>![]()
则![]()
∵![]() >
>![]() >
>![]() ∴
∴![]() >
>![]() ,
,![]() >
>![]()
∴![]() >
>![]() 即
即![]() >
>![]()
∴函数![]() 在
在![]() 上为增函数
8分
上为增函数
8分
(Ⅱ)由![]() >
>![]() 得
得![]() <0
10分
<0
10分
①当![]() >
>![]() ,即
,即![]() <
<![]() 时,
时,![]() <
<![]() <
<![]()
②当![]() =
=![]() ,即
,即![]() =
=![]() 时,无解
时,无解
③当![]() <
<![]() ,即
,即![]() >
>![]() 时,
时,![]() <
<![]() <
<![]()
∴当![]() <
<![]() 时,解集为
时,解集为![]()
当![]() =
=![]() 时,解集为空集
时,解集为空集
当![]() >
>![]() 时,解集为
时,解集为![]() 14分
14分
20、⑴第三次打开房门的结果有![]() 种,因此第三次打开房门的概率
种,因此第三次打开房门的概率![]() 4分
4分
⑵三次内打开房门的结果有![]() 种,因此,所求概率
种,因此,所求概率![]() 9分
9分
⑶方法一:因5把内有2把房门钥匙,故三次内打不开的结果有![]() 种,从而三次内打开的结果有
种,从而三次内打开的结果有![]() 种,所求概率
种,所求概率![]() 14分
14分
方法二:三次内打开的结果包括:三次内恰有一次打开的结果有![]() 种;三次内恰有2次打开的结果有
种;三次内恰有2次打开的结果有![]() 种。因此,三次内打开的结果有
种。因此,三次内打开的结果有![]() 种,所求概率
种,所求概率![]()
21、(Ⅰ)![]() ∵0<
∵0<![]() <1,∴0<
<1,∴0<![]() <
<![]() ,
,
令![]() >0,得
>0,得![]() <
<![]() <
<![]() ,令
,令![]() <0,得
<0,得![]() <
<![]() 或
或![]() >
>![]()
∴函数![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() 和
和![]() (5分)
(5分)
令![]() =0,得
=0,得![]() 或
或![]() ,
,
∴函数![]() 的极小值为
的极小值为![]() ,极大值为
,极大值为![]() (7分)
(7分)
(Ⅱ)由(Ⅰ)知![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
又∵0<![]() <1,∴
<1,∴![]() <
<![]() , ∴
, ∴![]() 在
在![]() 上是减函数, (9分)
上是减函数, (9分)
∴![]() ≤
≤![]()
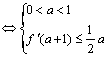 (11分)
(11分)
解得![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() (14分)
(14分)
22、⑴∵函数![]() 的函数图象过点
的函数图象过点![]() ,
,
∴函数![]() 的图象过点
的图象过点![]() ,则
,则![]() 。
。
又∵方程![]() 有两个相等的实数根,
有两个相等的实数根,
∴![]() ,即方程有等根
,即方程有等根![]() ,则
,则![]() 代入
代入![]() 得
得![]() ,故
,故![]() (5分)
(5分)
⑵∵![]() ,∴
,∴![]() ,即
,即![]()
∴![]() ,则
,则![]() (10分)
(10分)
⑶![]() ,
,![]()
![]() <
<![]()
![]() (16分)
(16分)