五·一家庭作业——解斜三角形
班级 学号 姓名
1、在直角三角形中，斜边是斜边上高的4倍，则两锐角的度数分别是 （ ）
A、30°，60° B、15°，75° C、20°，70° D、25°，65°
2、在ΔABC中，若
，
，则ΔABC的形状是
（ ）
A、等边三角形 B、锐角三角形 C、直角三角形 D、钝角三角形
3、在△ABC中，若b=2asinB,那么∠A的度数为 （ ）
A、30°或60° B、45°或60° C、60°或120° D、30°或150°
4、△ABC的三边长分别为AB=7，BC=5，CA=6，则·的值为： （ ）
A、19 B、－19 C、－18 D、－14
5、若
，且
, 那么
是
（ ）
A、直角三角形 B、等边三角形 C、等腰三角形 D、等腰直角三角形
6、己知
的夹角为
,则以
为邻边的平行四边形的一条对角线长为 ( )
A．15
B．
C．14
D．16
7、已知中，
且
，判定的形状。
8、已知的三个内角
成等差数列，且
，
。
（1）求角的大小 ；（2）如果
，求的一边
长及三角形面积。
9、如果△ABC的三边a、b、c满足
上的中线，求证：BE⊥CF。
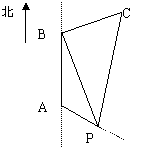10、如图，某海轮以30海里/小时的速度航行，在A点测得海面上油井P在南偏东60°，向北航行40分钟到达B点，测得油井P在南偏东30°，海轮改为北偏东60°的航向再航行80分钟到达C点，求PC间距离。
11、ΔABC中，若已知三边为连续正整数,最大角是钝角.
①求最大角；
②求以它的最大角为内角,夹此角的两边之和为4的平行四边形的最大面积.
12、在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市O（如图）的东偏南
）方向300km的海面P处，并以20km/h的速度向西偏北方向移动，台风侵袭的范围为圆形区域，当前半径为60km，并以10km/h的速度不断增大，问几小时后该城市开始受到台风的侵袭？