必修4第2章《平面向量》基础练习卷
班级______姓名___________
1、已知向量
（ ）
A．
B．
C．
D．
2、已知向量
则
的坐标是（ ）
A．
B．
C．
D．
3、已知
且
∥
，则x等于（ ）
A．3 B．
C．
D．
4、若
则与的夹角的余弦值为（ ）
A．
B．
C．
D．
5、若
，
与
的夹角是
，则
等于（ ）
A．12 B．
C．
D．
6、点
关于点
的对称点是（ ）
A．
B．
C．
D．
7、下列向量中，与
垂直的向量是（ ）
A．
B．
C．
D．
8、在平行四边形
中，
为
上任一点，则
等于（ ）
A．
B.
C.
D.
9、在平行四边形ABCD中，若
，则必有( )
A．
B．
或 C．ABCD是矩形 D．ABCD是正方形
10、已知点C在线段AB的延长线上，且
等于( )
A．3 B． C． D．
11、已知平面内三点
，则x的值为( )
A．3 B．
12、若三点
共线，则有（ ）
A
B 
C 
D 
13、设两个非零向量
不共线，且
共线，则k的值为( )
A．1 B．
C．
D．0
14、已知
，则点M的坐标是( )
A．
B．
C．
D．
15、已知
垂直，则
等于
16、已知等边三角形ABC的边长为1，则
17、设
是两个单位向量，它们的夹角是
，则
18、已知
19、设
＝(
,sinα)，
＝(cosα, ),且⊥，则tanα＝
.
20、若对n个向量
，存在n个不全为零的实数k1，k2，…，kn，使得
=
成立，则称向量为“线性相关”.依次规定，请你求出一组实数k1，k2，k3的值，它能说明
=(1,0), 
=(1,－1),
=(2,2) “线性相关”：k1，k2，k3的值分别是 ， ， .
21、已知
，求线段AB的中点C的坐标。
22、已知
的夹角为，求
23、平面向量
，已知∥，
，求、
及
夹角。
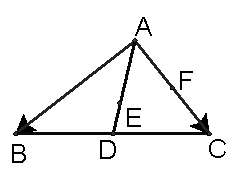
24、如图，在△ABC中，D、F分别是BC、AC的中点，AE=
AD，
=，
=， （1）用、分别表示向量
;（2）求证：B、E、F三点共线.
必修4第2章《平面向量》基础练习卷
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 答案 | D | B | C | A | C | C | A | B | C | D | C | C | C | B |
15、
16、
17、
18、10 19、
20、只要满足
即可
21、设
22、
23、
∥
，
24．（1）
，
，
，
，
.
（2）由（1）知，
，所以
∥
，又与有共同的起点，所以三点D、E、F共线.