高二理科数学第二学期期终考试卷
命题人: 蔡旺成 审核人: 曹齐平
(考试时间:120分钟 满分100分)
第Ⅰ选填部分(共48分)
一、选择题(每小题3分共36分,请将正确答案代号填在第Ⅱ卷卷首的答题栏中)
1、已知直线![]() 、
、![]() 和平面
和平面![]() ,则
,则![]() 的一个必要不充分的条件是( )
的一个必要不充分的条件是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 、
、![]() 与
与![]() 成等角
成等角
2、甲、乙、丙、丁、戊五人的比赛成绩中只知道丙比乙差,那么不同的排名方式有( )
A. 24种 B. 90种 C. 60种 D. 120种
3、已知![]() 平面
平面![]() ,
,![]() 为垂足,
为垂足,![]() 为斜线
为斜线![]() 在平面
在平面![]() 内的射影,
内的射影,![]() ,
,![]() ,
,![]() ,则
,则![]() 和平面
和平面![]() 所成的角为( )
所成的角为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、![]() 的各项系数之和大于
的各项系数之和大于![]() ,小于
,小于![]() ,则展开式中系数最大的项是( )
,则展开式中系数最大的项是( )
A.![]() B.
B. ![]() C.
C.
![]() D.
D.
![]() 或
或![]()
5、设![]() 、
、![]() 是两条异面直线,给出下列四个命题:①存在分别经过直线
是两条异面直线,给出下列四个命题:①存在分别经过直线![]() 和
和![]() 的两个互相平行的平面;②存在分别经过直线
的两个互相平行的平面;②存在分别经过直线![]() 和
和![]() 的两个互相垂直的平面;③存在经过直线
的两个互相垂直的平面;③存在经过直线![]() 且与
且与![]() 垂直的平面;④存在与
垂直的平面;④存在与![]() 、
、![]() 都平行且距离相等的平面;其中正确命题个数是( )
都平行且距离相等的平面;其中正确命题个数是( )
A.4个 B. 3个 C. 2个 D. 1个
6、设有编号为![]() 的四个球和编号为
的四个球和编号为![]() 的四个盒子,现将这四个球投放到四个盒子内,恰有两个盒子不放球的不同放法种数为( )
的四个盒子,现将这四个球投放到四个盒子内,恰有两个盒子不放球的不同放法种数为( )
A. 60 B. 72 C. 84 D. 120
7、一个盒子里装有相同大小的红球、白球共![]() 个,其中白球
个,其中白球![]() 个,从中任取
个,从中任取![]() 个,则概率为
个,则概率为![]() 的事件是(
)
的事件是(
)
A.没有白球 B.至少有一个白球 C.至少有一个红球 D.至多有一个白球
8、某班举行联欢会,原定的6个节目已排出节目单,演出前又增加了3个节目,若将这3
个节目插入原节目单中,则不同的插法总数为( )
A.504 B.210 C.336 D.378
9、5张卡片上分别写有A,B,C,D,E 5个字母,从中任取2张卡片,这两张卡片上的字母恰好是按字母顺序相邻的概率为( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
10、已知![]() ,从
,从![]() 到
到![]() 的映射
的映射![]() 满足:
满足:
①![]() ;②
;②![]() 中的元素在
中的元素在![]() 下不同的象有且只有3个,则适合条件的映射
下不同的象有且只有3个,则适合条件的映射![]() 的个数是(
)
的个数是(
)
A.6 B.10 C.60 D.360
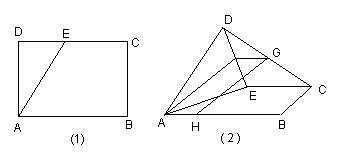
 11、在△ABC中,
11、在△ABC中,![]() 为
为![]() 中点,将△
中点,将△![]() 沿
沿![]() 折起,使
折起,使![]() 、
、![]() 间的距离为
间的距离为![]() ,如右图所示,则
,如右图所示,则![]() 到平面
到平面![]() 的距离为(
).
的距离为(
).
A.![]() B.
B.![]() C.1 D.2
C.1 D.2
12、三位数中,如果十位上的数字比百位上的数字和个位上的数字都大,则称这个数为凸数,如![]() 等,那么任取一个三位正整数恰好是无重复数字的三位凸数的概率是
( ).
等,那么任取一个三位正整数恰好是无重复数字的三位凸数的概率是
( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每小题3分共12分,请将正确答案代号填在第Ⅱ卷卷首的答题横线上)
13、某高中共有学生1200人,其中高一年级有500人,高二年级有400人,高三年级有300人,采用分层抽样方法抽取一个容量为60的样本,那么高一、高二、高三各年级抽取学生个数分别应为_______________________.
14、将正方形![]() 沿对角线
沿对角线![]() 折成一个直二面角,则异面直线AB和CD所成的角为__________________.
折成一个直二面角,则异面直线AB和CD所成的角为__________________.
15、一个四面体的所有棱长都为![]() ,四个顶点在同一个球面上,则此球的体积为___________________.
,四个顶点在同一个球面上,则此球的体积为___________________.
16、如图甲、乙、丙、丁为海上的四个小岛,要建三座桥,将这四个岛连接起来,不同的建桥方案共有______________种(用数字作答)

高二理科数学答题卷
第Ⅰ选填部分(共48分)
一、选择题:(36分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题:(12分)
13. ___________; 14.___________; 15. ___________; 16. __________.
第Ⅱ非选填部分(共52分)
三、解答题(共52分,解答应写出文字说明,证明过程或演算步骤.)
17、(6分)从5名男生和6名女生中,选出4人分别担任班长、宣传委员、劳动委员、生活委员组成班委会,若要求男生甲当班长,劳动委员一定要男生当,且班委会中至少有一名女生,则共有多少种不同的选法?
 |
18、(8分)已知![]() 展开式中的前三项系数成等差数列,
展开式中的前三项系数成等差数列,
求展开式中含![]() 的项
的项
 |
19、(8分)已知某种从太空飞船中带回的植物种子每粒成功发芽的概率都为![]() ,某植物研究所分两个小组分别独立开展该种子的发芽实验,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.(1)第一小组做了5次这种植物种子的发芽实验(每次均种下一粒种子),求至少有4次成功的概率;(2)第二小组做了若干次发芽实验(每次均种下一粒种子),如果在一次实验中种子发芽就停止实验,否则将继续进行下去,直到种子发芽成功为止,但发芽实验的次数最多不超过4次,求第二个小组所做的种子发芽的实验次数
,某植物研究所分两个小组分别独立开展该种子的发芽实验,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.(1)第一小组做了5次这种植物种子的发芽实验(每次均种下一粒种子),求至少有4次成功的概率;(2)第二小组做了若干次发芽实验(每次均种下一粒种子),如果在一次实验中种子发芽就停止实验,否则将继续进行下去,直到种子发芽成功为止,但发芽实验的次数最多不超过4次,求第二个小组所做的种子发芽的实验次数![]() 的概率分布列和期望。
的概率分布列和期望。
20、(8分)已知集合![]() ,在平面直角坐标系内,点
,在平面直角坐标系内,点![]() 中的
中的![]() ,且
,且![]() ,
,
(1)求点![]() 不在
不在![]() 轴上的概率;
轴上的概率;
(2)求点![]() 恰好在第二象限的概率。
恰好在第二象限的概率。
 |
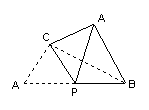
21、(10分)如图所示,在三棱锥![]() 中,
中,![]()
![]()
![]() 平面
平面![]() 平面
平面![]()
(1)求证![]() 平面
平面![]() ; (2)求点
; (2)求点![]() 到平面
到平面![]() 的距离。
的距离。
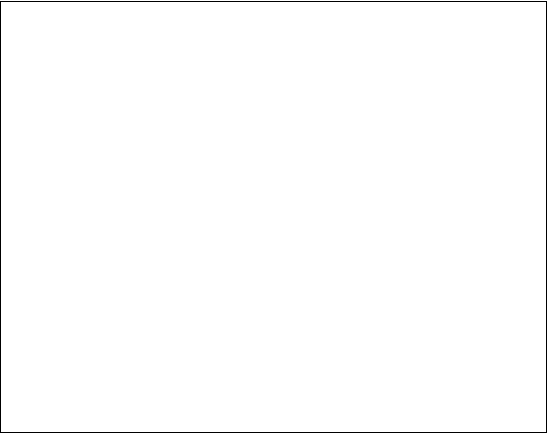
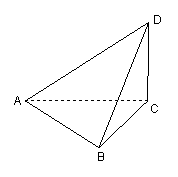
22、(12分)在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,沿
的中点,沿![]() 将△ADE折起,使二面角
将△ADE折起,使二面角![]() 为
为![]() ,如图所示
,如图所示
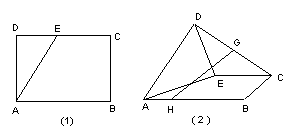
(1)若![]() 为
为![]() 中点,
中点,![]() ,求证
,求证![]() 平面
平面![]()
 (2)求
(2)求![]() 与平面
与平面![]() 所成角的大小;(3)求二面角
所成角的大小;(3)求二面角![]() 的大小。
的大小。
 |
高二理科数学参考答案及评分标准
一、选择题(每小题3分共36分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | C | C | A | B | C | B | A | B | C | C | B |
二、填空题(每小题3分12分)
13. 25,20,15; 14. ![]() 15.
15. ![]() ;
16. 16
;
16. 16
三、解答题(共52分,解答应写出文字说明,证明过程或演算步骤.)
17、(6分)班委会中至少有一名女生可分为两类:
一名女生进班委有![]() 种,两名女生进班委有
种,两名女生进班委有![]() 种,--------------------4分
种,--------------------4分
![]() (种) 即共有264选法。----------------------------6分
(种) 即共有264选法。----------------------------6分
18、(8分)解: ![]()
得前三项系数分别是![]() ,
,![]() ,
,![]()
前三项系数成等差数列,![]() 有
有![]() ----------------------3分
----------------------3分
解得![]() 或
或![]() (不合题意舍去)-----------------------------------5分
(不合题意舍去)-----------------------------------5分
![]()
由![]() 得
得![]() ---------------------------------------------------7分
---------------------------------------------------7分
![]() 所求项是
所求项是![]() -------------------------------------------------------8分
-------------------------------------------------------8分
19、(8分)解:(1)![]() 这5次实验是独立,
这5次实验是独立,
![]() 至少有3次实验成功的概率是
至少有3次实验成功的概率是![]() --------3分
--------3分
(2)![]() ,
,![]() ,
,![]() ,
,![]()
![]() 的概率分布如下:
的概率分布如下:
|
| 1 | 2 | 3 | 4 |
|
|
|
|
|
|
-------------------------------------------------------------------------3分
![]() -------------------------------------2分
-------------------------------------2分
20、(8分)(1)设事件![]() 表示点
表示点![]() 不在
不在![]() 轴上,则事件
轴上,则事件![]() 包含的结果数有
包含的结果数有![]() 种----------2分
种----------2分
![]() ----------------------------------------------------------4分
----------------------------------------------------------4分
(2)设事件![]() 表示点
表示点![]() 恰好在第二象限,则事件
恰好在第二象限,则事件![]() 包含的结果有
包含的结果有![]() 种------------------6分
种------------------6分
![]() ---------------------------------------------------------8分
---------------------------------------------------------8分
21、(10分)(1)在![]() △ABC中,求得
△ABC中,求得![]() ,
,![]() ,
,![]() ,
, ![]() 又
又![]() 平面
平面![]() 平面
平面![]()
![]()
![]() 平面
平面![]()
![]() --------3分
--------3分
又![]() ,
,![]() ,
,![]()
![]() 平面
平面![]() ---------------------4分
---------------------4分
(2)解法一:由![]() ,设点
,设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
则![]() ,------------------------------6分
,------------------------------6分
而![]() ,
,![]() 解得
解得![]()
![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]() -----------------------------------------8分
-----------------------------------------8分
解法二:作![]() 于
于![]() ,
,![]() 平面BCD,
平面BCD,![]() ,
,![]() 平面ABD,
平面ABD,![]() 的长为点
的长为点![]() 到平面
到平面![]() 的距离。------------------------------------------------------------6分
的距离。------------------------------------------------------------6分
在![]() △DCB中,由
△DCB中,由![]() 得
得![]() -------8分
-------8分
解法三:![]() 以
以![]() 为原点,分别以
为原点,分别以![]() 、
、![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,则
,则![]()
![]() ,
---------------------------------------------------------------------------------------5分
,
---------------------------------------------------------------------------------------5分
设![]() 为平面
为平面![]() 的法向量 , 则由
的法向量 , 则由![]()
得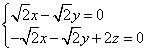
![]() 可取
可取![]() . -------------7分
. -------------7分
![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为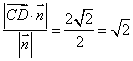
![]() 所求点
所求点![]() 到平面
到平面![]() 的距离为
的距离为![]() .-----8分
.-----8分
22、(12分)解:(1)如图(2),取![]() 中点
中点![]() ,连结
,连结![]() ,又
,又![]() . 又
. 又 ![]()
![]()
![]() ,
,![]() --------------------2分
--------------------2分
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
![]() 平面
平面![]() -----------------------------------4分
-----------------------------------4分
(2)如图(2),分别过点![]() 作
作![]() 平面ABCE于
平面ABCE于![]() ,
, ![]() 于
于![]() ,连结
,连结![]() ,则
,则![]() ,
,![]() 为二面角
为二面角![]() ─
─![]() ─
─![]() 的平面角,
的平面角,![]()
在![]() △
△![]() 中,
中,![]() ,
,
由![]() 得
得![]() .
.
在![]() △
△![]() 中,
中,
![]() --------------------------------2分
--------------------------------2分
. ![]() 平面
平面![]() 为所求角.在
为所求角.在![]() △
△![]() 中,
中, ![]()
![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() --------------------------4分
--------------------------4分
(3)如图(2),在平面![]() 内,作
内,作![]() 于
于![]() ,连接
,连接![]() ,
,
![]() 平面
平面![]() 为二面角
为二面角![]() ─
─![]() ─
─![]() 的平面角。
的平面角。
如图(1),作![]() 于
于![]() ,则由
,则由![]() △
△![]() ∽
∽![]() △
△![]()
得![]()
![]()
如图(2),在![]() △
△![]() 中,
中,![]()
又![]()
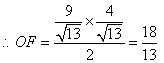 ------------------2分
------------------2分
如图(2)在![]() △
△![]() 中,
中,![]()
![]() 二面角
二面角![]() ─
─![]() ─
─![]() 的大
的大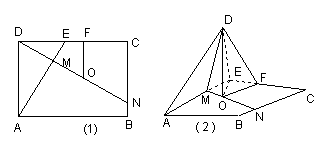 小为
小为![]() .--------------------------4分
.--------------------------4分