高二数学(理科)下学期期末考试试卷
注意:选择题答案用2B铅笔涂在答题卡上,填空题、解答题答案写在答题卷上。
一、选择题:(本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项符合题目要求)
1、已知复数![]() ,则
,则![]() 在复平面上对应的点位于 ( )
在复平面上对应的点位于 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2、“![]() ”是“
”是“![]() ”的( )
”的( )
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
3、在二项式![]() 的展开式中,含
的展开式中,含![]() 的项的系数是( )
的项的系数是( )
![]() .
. ![]()
![]() . 15
. 15 ![]() .
.![]()
![]() .
.![]()
4、某市组织一次高三调研考试,考试后统计的数学成绩服从正态分布,其密度函数
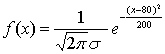 ,则下列命题不正确的是( )
,则下列命题不正确的是( )
A.该市这次考试的数学平均成绩为80分
B.分数在120分以上的人数与分数在60分以下的人数相同
C.分数在110分以上的人数与分数在50分以下的人数相同
D.该市这次考试的数学标准差为10
5、某人的密码箱上的密码是一种五位数字号码,每位上的数字可在0到9这10个数字中选取,该人记得箱子的密码1,3,5位均为0,而忘记了2,4位上的数字,只要随意按下2,4位上的数字,则他按对2,4位上的数的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6、已知A(-1,0),B(1,0),若点![]() 满足
满足![]()
( )
A.6 B.
7、某通讯公司推出一组手机卡号码,卡号的前七位数字固定,从“![]() ”到“
”到“![]() ”共
”共![]() 个号码.公司规定:凡卡号的后四位带有数字“
个号码.公司规定:凡卡号的后四位带有数字“![]() ”或“
”或“![]() ”的一律作为“优惠卡”,则这组号码中“优惠卡”的个数为( )
”的一律作为“优惠卡”,则这组号码中“优惠卡”的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 8、如图,在杨辉三角形中,斜线
8、如图,在杨辉三角形中,斜线![]() 的上方从1按箭头所示方向可以构成一个“锯齿形”的数列:1,3,3,4,6,5,10,…,记此数列的前
的上方从1按箭头所示方向可以构成一个“锯齿形”的数列:1,3,3,4,6,5,10,…,记此数列的前![]() 项之和为
项之和为![]() ,则
,则![]() 的值为( )
的值为( )
A.66 B.153
C.295 D.361
二、填空题:(本大题共6小题,每小题5分,共30分。把答案填在答题卷上)
9、![]()
10、在直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 是参数),若以
是参数),若以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,则曲线
轴的正半轴为极轴,则曲线![]() 的极坐标方程可写为________________.
的极坐标方程可写为________________.
11、已知![]() ,且
,且![]() ,则
,则![]() 的最大值为
的最大值为![]()
12、在约束条件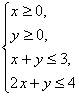 下,目标函数
下,目标函数![]() 的最大值是 .
的最大值是 .
13、动点P(x, y)满足![]() ,且P点的轨迹是椭圆,则a的取值范围是 .
,且P点的轨迹是椭圆,则a的取值范围是 .
14、等差数列有如下性质,若数列![]() 是等差数列,则当
是等差数列,则当![]() 也是等差数列;类比上述性质,相应地
也是等差数列;类比上述性质,相应地![]() 是正项等比数列,当数列
是正项等比数列,当数列![]() 时,数列
时,数列![]() 也是等比数列。
也是等比数列。
三、解答题:(本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤)
15、(12分)在某年一项关于16艘轮船的研究中,船的吨位区间从192吨到3246吨,船员的数目从5人到32人.船员人数![]() 关于船的吨位
关于船的吨位![]() 的线性回归方程为
的线性回归方程为![]()
(1)假设两艘轮船吨位相差1000吨,则船员平均人数相差多少?
(2)对于最小的船估计的船员数是多少?对于最大的船估计的船员数是多少?(保留整数)
16、(12分)已知![]() 顶点的直角坐标分别为
顶点的直角坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 是钝角,求
是钝角,求![]() 的取值范围.
的取值范围.
17、(14分)求由![]() 与直线
与直线![]() 所围成图形的面积.
所围成图形的面积.
 18、(14分)如图,面积为
18、(14分)如图,面积为![]() 的正方形
的正方形![]() 中有一个不规则的图形
中有一个不规则的图形![]() ,可按下面方法估计
,可按下面方法估计![]() 的面积:在正方形
的面积:在正方形![]() 中随机投掷
中随机投掷![]() 个点,若
个点,若![]() 个点中有
个点中有![]() 个点落入
个点落入![]() 中,则
中,则![]() 的面积的估计值为
的面积的估计值为![]() ,假设正方形
,假设正方形![]() 的边长为2,
的边长为2,![]() 的面积为1,并向正方形
的面积为1,并向正方形![]() 中随机投掷
中随机投掷![]() 个点,以
个点,以![]() 表示落入
表示落入![]() 中的点的数目.
中的点的数目.
(I)求![]() 的均值
的均值![]() ;
;
(II)求用以上方法估计![]() 的面积时,
的面积时,![]() 的面积的估计值与实际值之差在区间
的面积的估计值与实际值之差在区间![]() 内的概率.
内的概率.
附表:![]()
|
|
|
|
|
|
|
|
|
|
|
|
19、(14分)已知定义在正实数集上的函数![]() ,
,![]() ,其中
,其中![]() .设两曲线
.设两曲线![]() ,
,![]() 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(I)用![]() 表示
表示![]() ,并求
,并求![]() 的最大值;
的最大值;
(II)求证:![]() (
(![]() ).
).
20、(14分)若对于正整数![]() 、
、![]() 表示
表示![]() 的最大奇数因数,例如
的最大奇数因数,例如![]() ,
,![]() ,
,
并且![]() ,设
,设![]()
(Ⅰ)求S1、S2、S3 ;
(Ⅱ)求![]() ;
;
(III)设![]() ,求证数列
,求证数列![]() 的前
的前![]() 顶和
顶和![]() .
.
高二数学(理科)参考答案
一、选择题(每小题5分):1-4 D A C B 5-8 D B C D
二、填空题(每小题5分):9、![]() 10、
10、![]() 11、
11、![]()
12、7 13、(5,+∞) 14、![]()
三、解答题:
15、解:(1)依题意设船员平均人数相差为△y
则有△y=![]() 1-
1-![]() 2=0.0062×1000=6.2≈6
2=0.0062×1000=6.2≈6
(2)根据线性回归方程![]() 可得
………………………5分
可得
………………………5分
最小的船的估计船员![]() 3=9.5+0.0062×192≈11
3=9.5+0.0062×192≈11
最大的船的估计船员![]() 4=9.5+0.0062×3264≈30 ………………………11分
4=9.5+0.0062×3264≈30 ………………………11分
答:当两艘轮船的吨位相差1000吨时,船员平均人数相差6人,最小船的估计船员数是11人,最大船的估计船员人数是30人。 ………………………12分
16、解:(1)![]() ,
,![]() ,若c=5, 则
,若c=5, 则![]() ,
,
∴![]() ,∴sin∠A=
,∴sin∠A=![]() ;………………………6分
;………………………6分
(2)若∠A为钝角,则![]() 解得
解得![]() ,
,
∴c的取值范围是![]() ;
………………………12分
;
………………………12分
17、解:如图,作出曲线![]() ,
,![]() 的草图,所求面积为图中阴影部分的面积………3分
的草图,所求面积为图中阴影部分的面积………3分
 由
由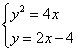 得交点坐标为
得交点坐标为![]() ,
,
(或答横坐标) …………………………5分
方法一:阴影部分的面积
![]() …………8分
…………8分
![]() …………………12分
…………………12分
![]() …………………………14分
…………………………14分
方法二:阴影部分的面积 ![]() ……………………………8分
……………………………8分
![]() …………………12分
…………………12分
= 9 ………………………………14分
18、解: 每个点落入![]() 中的概率均为
中的概率均为![]() . …………………………2分
. …………………………2分
依题意知![]() .…………………………4分
.…………………………4分
(Ⅰ)![]() .…………………………8分
.…………………………8分
(Ⅱ)依题意所求概率为![]() ,
,
![]()
![]()
![]()
![]() .…………………………14分
.…………………………14分
本小题主要考查函数、不等式和导数的应用等知识,考查综合运用数学知识解决问题的能力.
19、解:(Ⅰ)设![]() 与
与![]() 在公共点
在公共点![]() 处的切线相同.
处的切线相同.
![]() ,
,![]() , …………………………2分
, …………………………2分
由题意![]() ,
,![]() .
.
即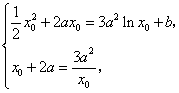 由
由![]()
得:![]() ,或
,或![]() (舍去).
(舍去).
即有![]() .…………………………4分
.…………………………4分
令![]() ,则
,则![]() .于是
.于是
当![]() ,即
,即![]() 时,
时,![]() ;
;
当![]() ,即
,即![]() 时,
时,![]() .
.
故![]() 在
在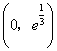 为增函数,在
为增函数,在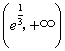 为减函数,
为减函数,
于是![]() 在
在![]() 的最大值为
的最大值为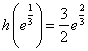 .…………………………7分
.…………………………7分
(Ⅱ)设![]() ,…………………………8分
,…………………………8分
则![]()
![]() .…………………………10分
.…………………………10分
故![]() 在
在![]() 为减函数,在
为减函数,在![]() 为增函数,
为增函数,
于是函数![]() 在
在![]() 上的最小值是
上的最小值是![]() .
.
故当![]() 时,有
时,有![]() ,即当
,即当![]() 时,
时,![]() .……………………14分
.……………………14分
20、解:(Ⅰ)![]() ……1分
……1分
![]() ……2分
……2分
![]() ……3分
……3分
(Ⅱ)![]() ,
,![]() ……4分
……4分
![]()
![]()
![]() ……5分
……5分
![]() ……6分
……6分
![]() ……7分
……7分
则![]()
![]() ……8分
……8分
![]()
![]() ……9分
……9分
(Ⅲ)![]() ……10分
……10分
![]()
![]()
![]() ……11分
……11分
![]() 当
当![]() 时,
时,![]() 成立 ……12分
成立 ……12分
当![]() 时,
时,![]() ……13分
……13分
![]()
![]() ……14分
……14分