高二数学第一学期期中考试试卷（文科）
试卷说明：
1．本试卷为高二数学文科试卷；
2．本试卷共8页，20小题，满分150分，考试时间120分钟；
3．选择题答案填涂在答题卡上，填空题和解答题填在试卷相应的位置上，其它地方答题或装订线外答题无效；
4．考试结束后上交试卷第二卷和答题卡。
第一卷
一、选择题（本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的）
1．已知p：
；q：
，则p是q的（ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
2．下列命题，其中真命题的个数是（ ）
①
②
③
④
A．0
B．
3．双曲线
两焦点之间的距离是（ ）
A
． B．
C．
D．
4．如果椭圆的长半轴长是3，焦距是4，那么椭圆的离心率是（ ）
A．
B.
C．
D．
5．当
时，方程
表示（ ）
A．圆 B．椭圆 C．双曲线 D．抛物线
6．以
为焦点的抛物线的标准方程为（ ）
A．
B.
C.
D.
7．已知等差数列的前
项和为
，若
，则
等于（ ）
A．18 B．
8．在
中，
，则
（ ）
A．
B．
C．
D．
9．已知椭圆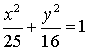
上一点
到椭圆一个焦点的距离为3，则到另一焦点的距离为（ ）
A．2 B．
10．椭圆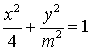
与双曲线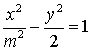
有相同的焦点，则
的值是（ ）
A．
B．
二、填空题（本大题共4小题，每小题5分，共20分。把答案填在题中横线上）
11．命题“
”的否定是_________________。
12.抛物线
的准线方程是______________________。
13．过椭圆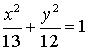
的右焦点与
轴垂直的直线与椭圆交于
两点，则
= ____________．
14.双曲线的渐近线方程为
，则双曲线的离心率是____________．
第二卷
三、解答题（本大题共6小题，满分80分。解答须写出文字说明，证明过程和演算步骤）
15．（本小题满分12分）求椭圆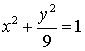
的长轴长，短轴长，顶点坐标，焦点坐标，离心率。
16．（本小题满分12分）在
中，已知
，
（1）求
和
；（2）求的面积。
17．（本小题满分14分）求标准方程：
（1）若椭圆长轴长与短轴长之比为2，它的一个焦点是
, 求椭圆的标准方程；
（2）若双曲线的离心率
，它的一个焦点是
，求双曲线的标准方程。
18. （本小题满分14分）设
是一个公差为
的等差数列，它的前10项和
且
成等比数列。
（1）证明：
；
（2）求公差
的值和数列的通项公式。
19.（本小题满分14分）在平面内，如果点
在运动过程中，总满足关系式
。
（1）点
的轨迹是什么曲线，为什么？
（2）写出此曲线的方程。
20．（本小题满分14分）已知椭圆
与直线
，
（1）当直线和椭圆有公共点时，求实数
的取值范围；
（2）求当直线与椭圆相切时的直线方程；
（3）求被椭圆截得最长弦所在的直线方程。
第二卷
|
11．______________________。12. ______________________。
13. ______________________。14. ______________________。
|
15．（本小题满分12分）
16．（本小题满分12分）
17．（本小题满分14分）
18. （本小题满分14分）
19.（本小题满分14分）
20.（本小题满分14分）