高二数学第一学期期中考试试卷
命题：迟立祥 审题：李彩芬
说明：本试卷满分100分，考试时间100分钟。学生答题时可使用学生专用计算器。
一、选择题（本大题共10小题，每小题4分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的）．
1.算法中用于“输入、输出”的框图是
（ ▲ ）
A.
B.
C.
D.
2.温州市某电器开关厂生产车间用传送带将产品送至下一工序，质检人员每隔半小时在传送带上取一件产品进行检验，则这种抽样方法是 （ ▲ ）
A.抽签法 B.系统抽样 C.分层抽样 D.随机数表法
3．
（ ▲ ）
A．
B．
C．
D．
4.某同学由
与
之间的一组数据求得两个变量间的线性回归方程为
，已知：数据的平均值为2，数据的平均值为3，则：
（ ▲
）
A．回归直线必过点（2，3）； B．回归直线一定不过点（2，3）；
C．点（2，3）在回归直线上方； D．点（2，3）在回归直线下方。
5．终边与角
终边关于轴对称的角的集合为
（ ▲ ）
A．
B．
C．
D．
6.在
中，
，则
等于
（ ▲ ）
A．
B．
C．
D． 
7．口袋里有5个大小完全一样的乒乓球，其中3个白色、2个黄色，一次取出2个，则至少有一个白色的概率为 （ ▲ ）
A．
B．
C．
D． 
8．已知函数
的最小正周期为
，则该函数的图象 （ ▲ ）
A．关于点
对称；
B．关于直线
对称；
C．关于点
对称；
D．关于直线
对称。
9.在区间[0，1]上任取两点
，方程
有实根的概率为 （ ▲ ）
A．
B．
C．
D．
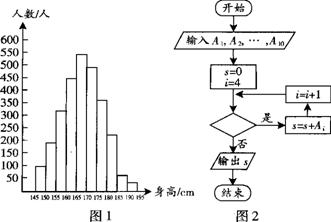10．图l是某县参加2007年高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为
、
、…、
(如表示身高(单位：
)在[150，155)内的学生人数)．图2是统计图l中身高在一定范围内学生人数的一个算法流程图．现要统计身高在160～180(含160，不含180)的学生人数，那么在流程图中的判断框内应填写的条件是 （ ▲ ）
A．
B．
C．
D．
二、填空题（本大题共7小题，每小题3分，满分21分）．
11.如果一组数据的最大值与最小值之差是21，取组距为3，则所分组数为__ ▲__ __。
12.运行下面方框中的程序，若输入的数字为-1，则输出
结果为__ ▲__ __。
13.已知
中，AB=4，AC=5，且的面积等于
5，则
=__
▲__ __。
14.若
，且
，则角
的取值
范围是__ ▲__ __。
15.已知一组数据：
，这组数据的平均数为10，
方差为2 ，则
的值为__ ▲__ __。
16. 已知
则
__ ▲__ __。
17.下列叙述：
①随机事件发生的频率就是这个随机事件发生的概率；
②我们称用计算机或计算器模拟试验的方法为蒙特卡罗方法；
③在一次试验中，任何两个可能出现的基本事件互斥；
④满足古典概型的随机试验，其所有可能出现的基本事件有有限个。
其中正确的叙述的序号为__ ▲__ __。
答 卷 纸
试场号：__________ 座位号:____________
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 15 | 16 | 17 | 18 | 19 | 20 | ||||
| 得分 | |||||||||
一、选择题（本大题共10小题，每小题4分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的）．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题（本大题共7小题，每小题3分，满分21分）．
11、__________________ 12、___________________ 13、____________________
14、__________________ 15、___________________ 16、____________________
17、__________________
三、解答题（本大题共5小题，满分39分．解答应写出文字说明．证明过程或演算步骤）．
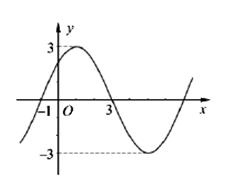18．（本小题满分7分）函数
的图象如下图所示。
（1）求解析式中
的值；
（2）该图像可由
的图像先向_____（填“左”或
“右”）平移_______个单位，再横向拉伸到原来的_______倍、
纵向拉伸到原来的______倍得到。
19.（本小题满分8分）调查某市出租车使用年限和该年支出维修费用（万元），得到数据如下：
| 使用年限 | 2 | 3 | 4 | 5 | 6 |
| 维修费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
（1） 求线性回归方程；
（2）由（1）中结论预测第10年所支出的维修费用。（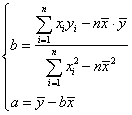
）
20.（本小题满分8分）某人抛掷一枚硬币，出现正反的概率都是，连续抛掷4次。
（1）求恰好出现3次正面的概率；
（2）求至少出现2次正面的概率。
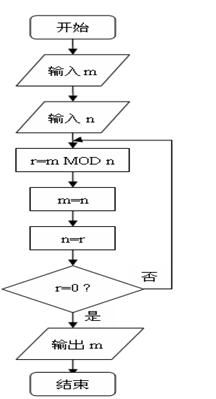
21.（本小题满分8分）执行右图中程序，回答下面问题。
|
___________________________;
（2）画出该程序的程序框图。
22.（文科，本小题满分8分）在中，已知内角A=
，边BC=
。设内角B=，
周长为。
（1）求函数
的解析式和定义域；
（2）求的最大值。
22.（理科，本小题满分8分）如图，已知是边长为1的正三角形，M、N分别是边AB 、AC上的点，线段MN经过的重心G。设
。
（1）试将
的面积（分别记为
与
）表示为的函数；
（2）求
的最大值与最小值。
高二数学试卷答案
一、选择题：（每小题给出的四个选项中，只有一项是符合题目要求的。）
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| B | B | D | A | C | C | D | A | D | B |
二、填空题：
11、
7 12、-5 13、
或
14、
15、4
16、
17、②③④
三、解答题（本大题共5小题，共39分，解答应写出文字说明、证明过程或演算步骤。）
18．（本小题满分7分）
解：（1）依图象有：A = 3，T = 8．∴
，∴
，
又由图象可知，当
时，
∴
，∴
．又
，∴
∴
∴A = 3，
，。
（2）左、
、
、3。
19、（本小题8分）
(1) 回归方程为：
(2) 预计第10年需要支出维修费用12.38 万元。
21.（本小题满分8分）
该试验满足古典概型。所有可能出现的基本事件有：全部出现正面时有1个基本事件、出现3个正面时有4个基本事件、出现2个正面时有6个基本事件、出现1个正面时有4个基本事件、不出现正面时有1个基本事件，共16个。
(1)设“出现3个正面”为事件A，所以，
。
（2）设“至少出现2次正面”为事件B，
。
21、（本小题8分）
（1） 6 (2)
22.（本小题满分8分）
（1）
=
定义域位
；
（2）当时，
。