高二数学第一学期期中考试试题
一、选择题（每题5分，共50分）
1、某班委会由4名男生与3名女生组成，现从中选出2人担任正副班长，至少有1名女生当选的概率为
A．
B．
C．
D．
2、若命题p的逆命题是q，命题q的逆否命题是r，则p与r的关系是
A、互为逆命题 B、互为否命题 C、互为逆否命题 D、 同一命题
3、椭圆的一焦点与短轴两顶点组成一个等边三角形，则椭圆的离心率为
A．
B．
C．
D．
4、从装有除颜色外完全相同的2个红球和2个白球的口袋内任取2个球，那么互斥而不对立的两个事件是
A．至少有1个白球，都是白球 B．至少有1个白球，至少有1个红球
C．恰有1个白球，恰有2个白球 D．至少有1个白球，都是红球
5、下列命题中正确的是
①“若x2＋y2≠0，则x，y不全为零”的否命题
②“正多边形都相似”的逆命题
③“若m>0，则x2＋x－m=0有实根”的逆否命题
④“若x=
，则x是无理数”的逆否命题
A、①②③④ B、①③④ C、②③④ D、①④
6、A是圆上固定的一点，在圆周上等可能地任取一点与A连结，弦长超过半径的概率为
A．
B．
C．
D．
7、设有n 个样本
,其标准差是
,另有n个样本
,且
( k = 1, 2, … , n
),其标准差为
,则下列关系正确的是
A. 
B.
C.
D. 
8、设
是双曲线
上的一点，双曲线的一条渐近线方程为
，
分别为双曲线的左右焦点，若
，则
等于（ ）
A．9 B．
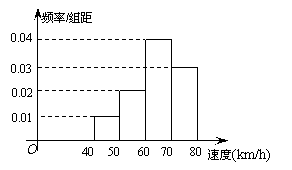9、如图是150辆汽车通过某路段时速度的频率分布
直方图，则速度在
的汽车大约有
A．100辆 B．80辆
C．60辆 D、40辆
10、下面的四个流程图经过执行后的结果是
的是
|
|
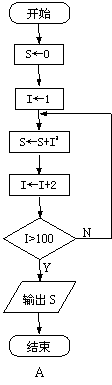
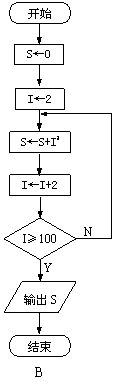
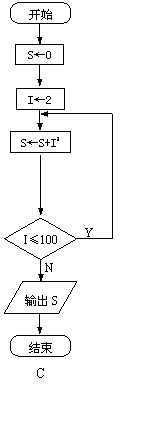
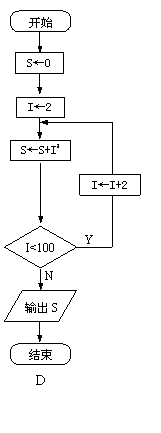
二、填空题（每题5分，共40分）
11、某班5次数学测验中，甲、乙两同学的成绩如下：
甲：90 92 88 92 88 乙：94 86 88 90 92
则甲、乙两人成绩相比较，得出结论是 稳定。
12、“10件产品中至少有一件次品”的否定是 。
13、设p：x
+x－6
0,q：
<0,则p是
q的 条件。
14、设椭圆
和双曲线
的公共焦点为F1、F2，P 是两曲线的一个公共点，则
的值等于 。
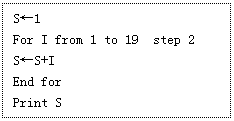15、右面是一个算法的伪代码，按这个伪代码写出的
程序在计算机上执行，最后运行的结果为
16、下列程序：
For I from 1 to 5 step 2
print
End for
输出的结果是 。
17、设双曲线C：
－
=1，椭圆的焦点恰为双 曲线C实轴上的两个顶点，椭圆与双曲线离心率为互为倒数，则此椭圆方程是________.
18、我国于07年10月24日成功发射嫦娥一号卫星，并经四次变轨飞向月球。嫦娥一号绕地球运行的轨迹是以地球的地心为焦点的椭圆。若第一次变轨前卫星的近地点到地心的距离为m，远地点到地心的距离为n，第二次变轨后两距离分别为2m、2n（近地点是指卫星到地面的最近距离，远地点是最远距离），则第一次变轨前的椭圆的离心率比第二次变轨后的椭圆的离心率 。（填变大或变小或不变）
三、解答题
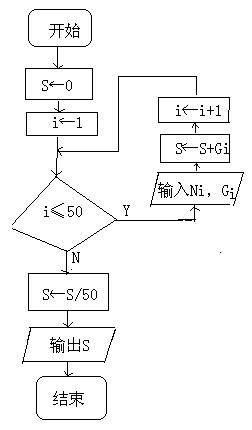
19、江苏省从2008年起实行新的高考模式，普通高中先进行必修科目学业水平测试，每科考分在90分（含90分）以上为A，75分到90分（含75分）为B，60分到75分（含60分）为C，60分以下为D。已知某班有50名同学，参加某科考试时的考号和成绩分别为Ni、Gi（i从1到50）。
（1）试完成画出求此班学生此科平均成绩的流程图（见答题纸）；
（2）试用伪代码表示输出每个学生的考号与等级的算法。（6分+8分）
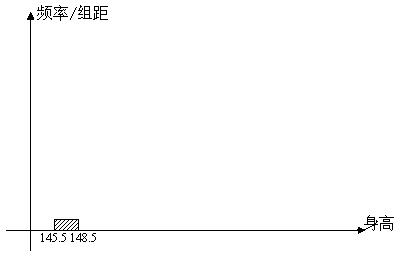
20、下表是某中学对本校初中二年级女生身高情况进行抽测后所得的部分资料(身高单位：cm,测量时精确到1cm)。已知身高在151cm (含151cm)以下的被测女生共3人．
（1）求所有被测女生总数；
（2）完成频率分布直方图，并在同一坐标系中画出折线图；
（3）估计初中二年级女生的平均身高。（4分+6分+4分）
| 分 组 | 频 率 |
| [145.5，148.5） |
|
| [148.5，151.5） | 0.04 |
| [151.5，154.5） | 0.08 |
| [154.5，157.5） | 0.12 |
| [157.5，160.5） | 0.30 |
| [160.5，163.5） | 0.20 |
| [163.5，166.5） | 0.18 |
| [166.5，169.5] | 0.06 |
0.02
21、将扑克牌4种花色的A、K、Q共12张洗匀。
（1）从中任意抽取两张，求抽出的都是A的概率；
（2）从中任意抽取两张，求抽出的至少有一张A的概率；
（3）从中任意抽取一张，然后放回再抽一张，求抽出的是花色不同概率。（4分+4分+5分+1分）
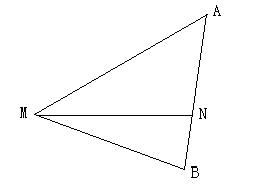
22、在△ABE中，AE=5，BE=4，AB=5，F为AB边上的一点。
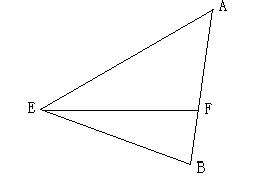（1）求以E、F为焦点， A、B都双曲线C的右支上的双曲线C的方程；
（2）P为双曲线C上异于顶点M、N的任意一点，直线PM、PN分别交y轴于G、H两点，O为原点，求证：OG×OH为定值。（7分+7分）
23、已知F1、F2 为椭圆C：
的左、右焦点，且若椭圆C的离心率为
，
（1）求m的值；
（2）若P为椭圆上一点，求PF1×PF2的最小值；
（2）若P为椭圆上一点，且△PF1F2为直角三角形，求△F1PF2的面积和周长。（3分+5分+6分）
高二数学试题 命题：滕于忠
一、选择题答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题答案
11、 。 12、 。
13、 。
14、 15、 16、
17、 18、
三、解答题
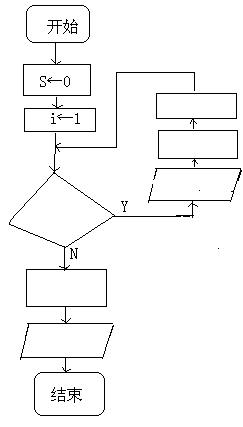
19、（1） （2）
20、
21、
|
22、
23、
高二数学期中考试试卷答案
CBACB BBBCD
11、甲；12、10件产品中都是正品；13、充分不必要；14、1/3
15、101；16、2，8，48；17、
；18、 不变
19、解： （1）
（2）For i From 1TO 50
Read Ni，Gi
If Gi≥90 Then
Print Ni；A
Else
If Gi≥75 Then
Print Ni；B
Else
If Gi≥60 Then
Print Ni；C
Else
Print Ni；D
EndIf
EndIf
EndIf
EndFor
20、（1）50
（2）略
（3）159.78cm
21、（1）1/11
（2）19/33
（3）3/4
22、（1）AF=3，BF=2（3分）建系（1分）x2－5y2/12=1（3分）
（2）G（0，y0/（1+x0）（2分）H（0，y0/（1－x0）（2分）
OG×OH=12/5（3分）
23、（1）m=9（3分）
（2）PF1×PF2=25－14x02/25，当x0=±5时，取最小值为9 （5分）
（3）△F1PF2周长为18（2分）
当∠PF1F2=900时，S=36/5；
当∠PF2F1=900时，S=36/5；（2分）
当∠PF2F1=900时，S=9。（2分）