两个平面的判定和性质

两个平面的判定和性质（）

1.命题：（1）如果一个平面内有两条直线平行于另一个平面，那么这两个平面平行；

（2）如果一个平面内有无数条直线平行于另一个平面，那么这两个平面平行；

（3）如果一个平面内有两条相交直线，分别平行于另一个平面内的两条直线，那么这两个平面平行；（4）如果一个平面内一个角（锐角或钝角）的两边和另一个平面内的一个角的两边分别平行，那么这两个平面平行。正确的是　　　　　　　　　  （　 ）

A.只有（1）（2）（4） B.只有（2）（3）（4） C.只有（3）（4）　D.四个命题都不正确

2．已知平面α//平面β，直线a//α，直线b//β，那么a与b的位置关系必定是（　 ）

  A平行或相交　　　　B 相交或异面　　　 C平行或异面　　　D平行、异面或相交

3．下列命题中不正确的是　　　　　　　　　　　　　　　　　　　　　 （　　）

  A垂直于同一条直线的两个平面平行

B垂直于同一个平面的两条直线互相平行

C过平面α的一条斜线的平面β与α一定不垂直

D平行于同一平面的两个平面平行。

4．已知平面α//平面β，直线a、b分别与α、β所成的角相等，

则直线a,b的位置关系是　　　　　　　 。

5．经过平面外一点可以作　　　 个平面平行于这个平面；可以作　　　　　 条直线平行于这个平面。

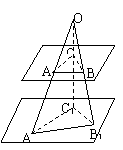
6．如图，平面，自点O引三条直线分别交α、β

于点A、B、C和点A₁、B₁、C₁，则△ABC与△A₁B₁C₁

的关系是　　　　　　  。

7.已知正方形ABCD—，求证：平面∥平面

两个平面平行的判定和性质

1.如果一个平面内有无数条直线与另一个平面平行，那么这两个平面　　　 （　　 ）

 A.平行　　　　B.相交　　　　 C.重合　　　　　 D.平行或相交

2.过平面外一条直线与平行的平面的个数是　　　　　　　　　　　 （　　 ）

  A.只有一个　 B.至少有一个　 C.至多有一个　　 D.没有

3.下列条件中，可判断平面α与β平行的是　　　　　　　　　　　　　　　　　　　　　　　　　 （　　 ）

　　　　　　　　　　　　　　　　　　　 A．α、β都垂直于平面r.

　　　　　　　　　　　　　　　　　　　 B．α内存在不共线的三点到β的距离相等.

　　　　　　　　　　　　　　　　　　　 C．l，m是α内两条直线，且l∥β，m∥β.

D．l，m是两条异面直线，且l∥α，m∥α, l∥β，m∥β.

4 设m、n为两条直线，、为两个平面，A为一点，给出以下命题：

（1）　　　 若则m、n必为异面直线；

（2）　　　 若∥，∥n，则n∥；

（3）　　　 ∥，∥，则∥；

（4）　　　 若m∥∥，则m∥n;

其中正确命题的个数为　　　　  。

5.已知平面α//平面β，直线a、b分别与α、β所成的角相等，

则直线a,b的位置关系是　　　　　　　　

6.别在两个平面内的三角形都有两条边与同一条直线垂直，则这两个三角所在

面的位置关系是

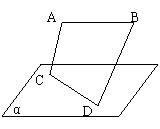
7. 已知AB与CD为异面线段，CD平面α，AB//α，M、N分别是线段AC与BD的中点，求证：MN//平面α。

参考答案（1A）

一、选择题：　　　 CDC

二、填空题：4、不确定。　5、一；无数。　　 6、相似。

三、解答题：7、略。

参考答案（1B）

一、选择题：　　　 DCD

二、填空题：4、0。　　5、不确定。　6、平行。

三、解答题：7、略。