两个平面平行的判定和性质（
1.在正方体ABCD—A1B
A 邻边不等的平行四边形； B 菱形但不是正方形 （ ）
C 邻边不等的矩形 D 正方形
2. a、b、c为三条不重合的直线，
为三个不重合的平面，现给出六个命题：
（1）a∥c, b∥c 
a∥b
(2)a∥
, b∥ a∥b
（3）
∥c, 
∥c ∥
(4) ∥ , ∥ ∥
(5) a∥c , ∥c a∥
(6) a∥, ∥ a∥
其中正确的命题是
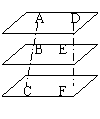3. a、b表示直线，表示平面，下列命题中正确的是
（1）
∥b，则∥
（2）
⊥
b⊥且a∥b，则∥
（3）
⊥⊥，b⊥，b⊥，则∥
（第4题）
（4）与
相交且所成的角相等，则∥
4．如图，直线AC、DF被三个平行平面α、β、γ所截，已知
AB=2，BC=3，EF=4，则DF= 。
5.已知点S是正三角形ABC所在平面外的一点，且SA=SB=SC， SG为
上的高，D、E、F分别是AC、BC、SC的中点，试判断SG与平面DEF的位置关系，并证明。
6.P是所在平面外一点，
、
、
分别是
、
、
的重心
（1）
求证：平面 
∥平面ABC
（2）
（2）求
：
两个平面平行的判定和性质（
1.设有不同的直线，a、b和不同的平面， 给出下列三个命题，其中正确的个数是
（1）a∥，b∥则a∥b （2）若a∥，a∥则
∥ （3）若⊥，⊥则
∥
A. 0
B.
2. 是两个平面，
、
是两条直线，那么∥的一个充分而不必要的条件是
A.
∥，m∥ B. 
∥m
C. ⊥,m⊥且 ∥m
D . ∥，m∥，且 ∥m
3.，且的距离为d，
，则在面内
（ ）
A.有且只有一条直线与a的距离为d B.所有直线与a的距离都等于d
C.有无数条直线与a的距离等于d D.所有直线与a 距离都不等于d
4. 已知AB、CD是夹在两平行平面之间的两条线段，AB⊥CD，AB=2，AB与平面成300角，则线段CD的取值范围是
（ ）
A.
B.
C.（1，
）
D.
5. 若∥，AB⊥, AB⊥,
直线a、b,
且a∥b，A到a的距离是2，B到b的距离是5，AB=4，则a、b间的距离是
6. 若∥，
，直线AB与CD交于点S，且AS=8，BS=9，CD=34
（1）当S在之间时，SC=
（2）当S不在之间时，SC=
7.已知
∥∥，A、D
，C、F
，AC、DF分别交平面于B、E。
（1） 求证：
（2） 设AF交于M，若
=1，异面直线AD与CF所成角为
，AD=2，CF=4，求
参考答案（
一、选择题： B
二、填空题：2、1；4。 3、2；3。 4、
。
三、解答题：5、平行。 6、（1）略；（2）1：9。
参考答案（2B）
一、选择题： ACCB
二、填空题：5、5或
； 6、16或272。
三、解答题：7、（1）略；（2）
。