排列组合、二项式定理、概率测试卷

高二数学抽测（1）---排列组合、二项式定理、概率测试卷

一、选择题：(本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.)

1．从7人中选派5人到10个不同岗位的5个中参加工作，则不同的选派方法有　　　　　　  （　　）

　　A、种　　　 B、种　　　C、种　　 D、

2．以1，2，3，…，9这九个数学中任取两个，其中一个作底数，另一个作真数，则可以得到不同的对数值的个数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  （　　）

A、64　　　　　　 B、56　　　　　 C、53　　　　　  D、51

3．设，则S等于　　　　　　　　　　　　　　  （　　）

　　A、x⁴　　　　　　　 B、x⁴+1　　　　　  C、(x-2)⁴　　　　 D、x⁴+4

4．学校要选派4名爱好摄影的同学中的3名参加校外摄影小组的3期培训（每期只派1名），由于时间上的冲突，甲、乙两位同学都不能参加第1期培训，则不同的选派方式有　　　　　　　　　　  （　　）

　　A、6种　　　　　　　 B、8种　　　　  C、10种　　　　　 D、12种

5．甲、乙、丙三个人负责一个计算机房周一至周六的值班工作，每天1人，每人值班2天。如果甲同学不排周一，乙同学不排值周六，则可以排出不同的值班表有　　　　　　　　　　　　　　　  （　　）

　　A、36种　　　　 　　B、42种　　　　  C、50种　　　　  D、72种

6．从1，2，……，9这九个数中，随机抽取3个不同的数，则这3个数的和为偶数的概率是　 （　　）

A、　　　　　　　B、　　　　　　　 C、　　　　 　D、

7．(1-2x)⁷展开式中系数最大的项为　　　　　　　　　　　　　　　　　　　　　　　　　  （　　）

A、第4项　　　　 B、第5项　　　　C、第7项　　　 D、第8项

8．事件A与事件B互斥是事件A、事件B对立的　　　　　　　　　　　　　　　　　　　　  （　　）

A.充分不必要条件；　　 B.必要不充分条件；

C.充分必要条件；　　　 D.既不充分也不必要条件

9．设有甲、乙两把不相同的锁，甲锁配有2把钥匙，乙锁配有2把钥匙，这4把钥匙与不能开这两把锁的2把钥匙混在一起，从中任取2把钥匙能打开2把锁的概率是　　　　　　　　　　　　　  （　　）

A、4/15　　　　　 B、2/5　　　　  C、1/3　　　　　 D、2/3

10．若展开式中含有常数项，则n的最小值是　　　　　　　　　　　 （　　）

　　　 A、4　　　　　 B、3　　　　　  C、12　　　　　 D、10

11．将一颗质地均匀的骰子（它是一种各面上分别标有点数1，2，3，4，5，6的正方体玩具）先后抛掷3次，至少出现一次6点向上的概率是　　　　　　　　　　　　　　　　　　　　　　　　　  （　　）

A、 　　　B、 　　　　C、 　　　 　D、

12．四面体的顶点和各棱中点共10个点, 在其中取4个不共面的点, 则不同的取法共有　　　 (　　 )

A． 150种　　　　　　 B． 147种　　　　  C． 144种　　　　  D． 141种

二、填空题：（本大题共4小题，每小题4分，共16分）

13．四封信投入3个不同的信箱，其不同的投信方法有　　　　 种　

14．若, 则n的值为　　　　　 .

15．若以连续投掷两次骰子分别得到的点数m、n作为点P的坐标，则点P落在直线x+y=5下方的概率

是________

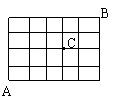
16．某城市的交通道路如图，从城市的东南角A到城市的西北角B，

不经过十字道路维修处C，最近的走法种数有_________________。

三、解答题（本大题共6小题，共74分解答应写出文字说明、证明过程或演算步骤）

17．（本小题满分12分）用0，1，2，3四个数字组成没有重复数字的自然数，把这些自然数从小到大排成一个数列，问1230是这个数列的第几项？

18、（本小题满分12分）在二项式的展开式中，前三项系数的绝对值成等差数列

（1）求展开式的第四项；

（2）求展开式的常数项；

（3）求展开式中各项的系数和。

19．（本小题满分12分）从5双不同的鞋中任意取出4只，求下列事件的概率：

（1）所取的4只鞋中恰好有2只是成双的；

（2）所取的4只鞋中至少有2只是成双的

20．（本小题满分12分）袋中有5个白球，3个黑球，从中任意摸出4个，求下列事件发生的概率：

（1）摸出2个或3个白球；（2）至少摸出1个白球；（3）至少摸出1个黑球.

21．（本小题满分12分）已知的展开式的系数和比的展开式的系数和大992,

求的展开式中:①二项式系数最大的项;②系数的绝对值最大的项

22、（本小题满分14分）设有编号为1，2，3，4，5的五个球和编号为1，2，3，4，5的五个盒子，现将这五个球放入5个盒子内

（1）只有一个盒子空着，共有多少种投放方法？

（2）没有一个盒子空着，但球的编号与盒子编号不全相同，有多少种投放方法？

　 （3）每个盒子内投放一球，并且至少有两个球的编号与盒子编号是相同的，有多少种投放方法？

柔石中学高二数学抽测（1）---排列组合、二项式定理、概率测试卷答案

一、选择题：(本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.)

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	D	C	A	D	B	C	B	B	A	A	C	D

二、填空题：（本大题共4小题，每小题4分，共16分）

13.　　　 　　　 　　　　　　14.　　　　 7　　　　

15.　　_______　　　　_ 　　　16.　　　　 _66　　　

三、解答题（本大题共6小题，共74分解答应写出文字说明、证明过程或演算步骤）

17．（本小题满分12分）用0，1，2，3四个数字组成没有重复数字的自然数，把这些自然数从小到大排成一个数列，问1230是这个数列的第几项？

17．解：分类讨论

1）1位自然数有4个；

2）2位自然数有9个，其中①含零 “XO” 型有3个，

②不含零 “XX”型有；

3）3位自然数有18个，即

4）4位自然数中， “10xx”型有个

1203，1230共有4个

由分类计数原理知，1230是此数列的第4+9+18+4=35项.

18、（本小题满分12分）在二项式的展开式中，前三项系数的绝对值成等差数列

（1）求展开式的第四项；

（2）求展开式的常数项；

（3）求展开式中各项的系数和。

解：18、展开式的通项为，r=0，1，2，…，n

 由已知：成等差数列

∴

∴ n=8　　　　　　　　　　　　　　　　　  ……2分

　 （1）　　　　  　　　　　　　　　 ……4分

　 （2） 由 则r=4　　　　　　 ……8分

（3）令x=1，各项系数和为　　　　　　 ……12分

19．（本小题满分12分）从5双不同的鞋中任意取出4只，求下列事件的概率：

（1）所取的4只鞋中恰好有2只是成双的；

（2）所取的4只鞋中至少有2只是成双的

解：基本事件总数是=210

（1）恰有两只成双的取法是=120

∴所取的4只鞋中恰好有2只是成双的概率为

(2)事件“4只鞋中至少有2只是成双”包含的事件是“恰有2只成双”和“4只恰成两双”，恰有两只成双的取法是=120，四只恰成两双的取法是=10

∴所取的4只鞋中至少有2只是成双的概率为

20．（本小题满分12分）袋中有5个白球，3个黑球，从中任意摸出4个，求下列事件发生的概率：

（1）摸出2个或3个白球；

（2）至少摸出1个白球；

（3）至少摸出1个黑球.

解：从8个球中任意摸出4个共有C种不同的结果.记从8个球中任取4个，其中恰有1个白球为事件A₁，恰有2个白球为事件A₂，3个白球为事件A₃，4个白球为事件A₄，恰有i个黑球为事件B_i，则：

（1）摸出2个或3个白球的概率

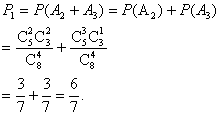
（2）至少摸出1个白球的概率

P₂=1－P（B₄）=1－0=1

（3）至少摸出1个黑球概率

P₃=1－P（A₄）=1

21．（本小题满分12分）已知的展开式的系数和比的展开式的系数和大992,求的展开式中:①二项式系数最大的项;②系数的绝对值最大的项

解：由题意,解得

 ①的展开式中第6项的二项式系数最大,

即

②设第项的系数的绝对值最大,

则

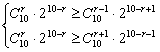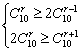 ∴,得,即

 ∴,∴,故系数的绝对值最大的是第4项即

22、（本小题满分14分）设有编号为1，2，3，4，5的五个球和编号为1，2，3，4，5的五个盒子，现将这五个球放入5个盒子内

（1）只有一个盒子空着，共有多少种投放方法？

（2）没有一个盒子空着，但球的编号与盒子编号不全相同，有多少种投放方法？

　 （3）每个盒子内投放一球，并且至少有两个球的编号与盒子编号是相同的，有多少种投放方法？

解：22、（1）C₅²A_­5⁴=1200（种）　　　　　　　　  ……4分

（2）A₅⁵-1=119（种）　　　　　　　　　　　 ……8分

（3）满足的情形：第一类，五个球的编号与盒子编号全同的放法：1种

第二类，四个球的编号与盒子编号相同的放法：0种

第三类，三个球的编号与盒子编号相同的放法：10种

第四类，二个球的编号与盒子编号相同的放法：2C₅²=20种

∴ 满足条件的放法数为：

　 1+10+20=31（种）　　　　　　　　　  ……14分

柔石中学高二数学抽测（1）---排列组合、二项式定理、概率答题卷

班级________学号_______姓名__________________

题号	一	二	三 17　　 18　　 19　　 20　　21　　 22	总分
得分

一、选择题：(本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.)

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二、填空题：（本大题共4小题，每小题4分，共16分）

13.　  _______　　　　_ 　　　　　　14.　　_______　　　　_  

15.　　_______　　　　_ 　　　　　　 16.　　_______　　　　_  

三、解答题（本大题共6小题，共74分解答应写出文字说明、证明过程或演算步骤）

17．（本小题满分12分）用0，1，2，3四个数字组成没有重复数字的自然数，把这些自然数从小到大排成一个数列，问1230是这个数列的第几项？

18、（本小题满分12分）在二项式的展开式中，前三项系数的绝对值成等差数列

（1）求展开式的第四项；

（2）求展开式的常数项；

（3）求展开式中各项的系数和。

19．（本小题满分12分）从5双不同的鞋中任意取出4只，求下列事件的概率：

（1）所取的4只鞋中恰好有2只是成双的；

（2）所取的4只鞋中至少有2只是成双的

20．（本小题满分12分）袋中有5个白球，3个黑球，从中任意摸出4个，求下列事件发生的概率：

（1）摸出2个或3个白球；

（2）至少摸出1个白球；

（3）至少摸出1个黑球.

21．（本小题满分12分）已知的展开式的系数和比的展开式的系数和大992,求的展开式中:①二项式系数最大的项;②系数的绝对值最大的项

22、（本小题满分14分）设有编号为1，2，3，4，5的五个球和编号为1，2，3，4，5的五个盒子，现将这五个球放入5个盒子内

（1）只有一个盒子空着，共有多少种投放方法？

（2）没有一个盒子空着，但球的编号与盒子编号不全相同，有多少种投放方法？

　 （3）每个盒子内投放一球，并且至少有两个球的编号与盒子编号是相同的，有多少种投放方法？