排列组合、二项式定理、概率单元测试卷
班级 姓名 学号
一、选择题（每题3分，计36分）
1．设集合A=
，B=
，则从A到B的不同映射的个数为---------------（ ）
A、
B、
C、
D、
2．将标号为
的10个球放入标号为的10个盒子里，恰好3个球的标号与所在盒子的标号不一致的放法种数为-----------------------------------------------------（ ）
A、120 B、240 C、360 D、720
3．设
，则S等于-----------------------（ ）
A、x4 B、x4+1 C、(x-2)4 D、x4+4
4．学校要选派4名爱好摄影的同学中的3名参加校外摄影小组的3期培训（每期只派1名），由于时间上的冲突，甲、乙两位同学都不能参加第1期培训，则不同的选派方式有（ ）
A、6种 B、8种 C、10种 D、12种
5．甲、乙、丙三个人负责一个计算机房周一至周六的值班工作，每天1人，每人值班2天。如果甲同学不排周一，乙同学不排值周六，则可以排出不同的值班表有------------（ ）
A、36种 B、42种 C、50种 D、72种
6．从1，2，……，9这九个数中，随机抽取3个不同的数，则这3个数的和为偶数的概率是---------------------------------------------------------------------------------------------（ ）
A、
B、
C、
D、
7．(1-2x)7展开式中系数最大的项为---------------------------------------------------------（ ）
A、第4项 B、第5项 C、第7项 D、第8项
8．在一次足球赛中，某小组共有5个球队进行双循环赛（每两队之间赛两场），已知胜一场得3分，平一场得1分，负一场得0分。积分多的前两名可出线（积分相等则要比净胜球数或进球总数），赛完后，一个队的积分可出现的不同情况种数为----------------（ ）
A、22 B、23 C、24 D、25
9．一台X型号的自动机床在一小时内不需要工人照看的概率为0.8000，有四台这种型号自 动机床各自独立工作，则一小时内至多有2台机床需要工人照看的概率是---------（ ）
A、0.1536 B、0.1808 C、0.5632 D、0.9728
10．. 若
展开式中含有常数项，则n的最小值是----------------（ ）
A、4 B、3 C、12 D、10
11．将一颗质地均匀的骰子（它是一种各面上分别标有点数1，2，3，4，5，6的正方体玩具）先后抛掷3次，至少出现一次6点向上的概率是-------------------------------------- ( )
A、 B、 C、 D、
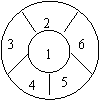12．如图：用四种不同的颜色给标有数字的6个区域染色，要求相邻的区域不能染同色，则不同的染色方法有--------------------------------------------------------------------------------（ ）
A、720 B、240 C、120 D、96
二、填空题（每题4分，计16分）
13．设
，则
。
14．我国已经正式加入WTO，包括汽车在内的进口商品将最多在五年内把关税全部降低到世贸组织所要求的水平，其中有21%的进品商品恰好5年关税达到要求，18%的进口商品恰好4年达到要求，其余的进口商品将在3年或3年内达到要求，则进口汽车在不超过4年的时间内关税达到要求的概率为_______________________。
15．在
的展开式中，含
项的系数是
。
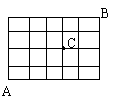
16．某城市的交通道路如图，从城市的东南角A到城市的西北角B，
不经过十字道路维修处C，最近的走法种数有_________________。
三、解答题：
17． 6女，4男中随机选出3位参加测验．每位女同学能通过测验的概率为0.8，每位男同学能通过测验的概率为0.6．试求：
⑴选出的3位同学中，至少有一位男同学的概率；
⑵10位同学中的女同学甲和男同学乙同时被先选中且通过测验的概率．
18．如果a(1-a)4+a2(1+2a)k+a3(1+3a)12的展开式中含a4项的系数为114，求正整数k的值。
19．某地举行篮球比赛，其中男子篮球总决赛在雄风队与豪杰队之间角逐，采用七局四胜制，若有一队胜4场，由此队获胜且结束比赛，因而队实力非常接近，在每场比赛中两队获胜是等可能的。据以往资料统计，每场比赛组织者可获门票收入5万元，两队决出胜负后，问：
（1）求组织者在此次决赛中获门票收入为20万元的概率。
（2）求组织者在此次决赛中获门票收入不少于30万元的概率。
20．某人有5把钥匙，其中只有一把房门钥匙，但忘记了开房门的是哪一把，于是，他逐把不重复地试开，问：（1）恰好第三次打开房门锁的概率是多少？
（2）三次内打开的概率是多少？
（3）如果5把内有2把房门钥匙，那么三次内打开的概率是多少？
21．已知数列
是等比数列，
，公比q是
的展开式的第二项（按x的降幂排列）（1）求数列的通项
与前n项和
。
（2）若
，求
。
22．平面上两个质点A、B 分别位于（0，0），（2，2），在某一时刻同时开始，每隔1秒钟向上下左右任一方向移动1个单位，已知质点A向左右移动的概率都是
向上下移动的概率分别是
和
质点B向各个方向移动的概率是
求：（1）4秒钟后A到达C（1，1）的概率；
（2）三秒钟后，A，B同时到达D（1，2）的概率.
排列组合、二项式定理及概率单元试卷答案
一、选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| D | B | A | D | B | B | C | C | D | A | C | C |
二、填空题
| 13 | 14 | 15 | 16 |
| 1023 | 0.79 | 240 | 66 |
三、解答题
17．解：⑴随机选出的3位同学中，至少有一位男同学的概率为
；
⑵甲、乙被选中且能通过测验的概率为
18．由已知得:
，即: 
19．（1）门票收入20万无，必须比赛四场，且能决出胜负
两种可能：一是雄风队连胜两场，二是豪杰队连胜四场，故
门票收入为20万元的概率
;门票收入为25万元的概率
故门票收入不少于30万元概率为
20．解：5把钥匙，逐把试开有
种等可能的结果。
（1）第三次打开房门的结果有
种，因此第三次打开房门的概率P（A）=
=
（2）三次内打开房门的结果有3种，因此第三次打开房门的概率P（A）=
=
（3）解法一：三次内打开的结果包括：三次内恰好有一次打开的结果
；三次内恰好有二次打开的结果
。因此，所求的概率P（A）=
解法二：因5把内有2把房门钥匙，故三次内打不开的结果有
种，从而三次内打开的结果有
种，所求概率P（A）=
=
21．（1）q=
，所以
（i）当x=1时，
。
(ii)当
时，
。
（2）(i)当x=1时，＝
(ii)当时，＝
＝
＝
。
22.
