排列组合和概率测试卷
姓名 成绩
一、选择题（本大题共
个小题，每小题
分，共
分，每题给出的四个选项中有且只有一个是符合题目要求的）
1．把
个人分成前后三排，每排
人，排法种数为
（ ）
（A）
（B）
（C）
（D）以上都不对
2．
，且它们最大公约数等于
，则
的公约数的个数为 （ ）
（A）
（B）
（C）
（D）
3．用四个数字
组成没有重复数字的四位数，再将这些四位数按照从小到大的顺序排列成一个数列，则这个数列的第
项是
（ ）
（A）
（B）
（C）
（D）
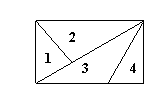4．用五种不同的颜色给如图的四个区域涂色，每个区域涂一种颜色，相邻的区域涂不同的颜色，则涂色的方法共有
（ ）
（A）
种
（B）
种
（C）
种
（D）
种
5．
其中
是（ ）
（A）
（B）
（C）
（D）
6．从集合
到集合
作一一映射，若
的象不是
的原象不是
，则这样的一一映射有
（ ）
（A）
个
（B）
个
（C）
个
（D）
个
7．若
则k的取值范围是
（ ）
（A）
（B）
（C）
（D）
8．从全体3位整数中任取一数，则此数以2为底的对数也是正整数的概率为 （ ）
（A）
（B）
（C）
（D）以上全不对
9．设
，则
的反函数
等于（ ）
（A）
（B）
（C）
（D）
10.从
这
个数中，任取个不同的数，分别作为函数
中的
的值，其中所得的函数恰为偶函数的概率是
（ ）
（A）
（B）
（C）
（D）
二、填空题（本大题共5个小题，每小题分，共
分）
11．制作某种零件，必须经过
道加工工序，若其中甲工序必须排在乙工序之前，丙工序必须排在乙工序之后（都不一定相连），则加工流程共有
种。
12．已知
是两条异面直线，其中
上有个点，
上有
个点，若从这个点中任取 个点构成一个平面，共可组成
个平面。
13．已知
的展开式中
的系数为
，常数的值为
。
14．袋中装有只白球和
只黑球，每次取一个，有返回的取两次，在第一次取到白球的条件下，第二次取到白球的概率是
。
15．马路上有编号为
的九只路灯，为节约用电，可以把其中的三只路灯关掉，但不能同时关掉相邻的两只或三只，也不能关掉两端的路灯，则应关路灯的概率是
。
三、解答题(本大题共个小题，共分)
16.（本题8分）已知
的展开式中，前三项的系数成等差数列，求展开式中所有有理项.
17.（本题6分）某学会进行换届选举，要从甲、乙、丙、丁四人中选出人担任不同的职务.规定上届任职的甲、乙、丙三人都不能任原职，求不同的任职方法数.
18.（本题10分）从
五个数字中，任意有放回地连续抽取三个数字，求下列事件的概率：
(1)三个数字完全不同；
(2)三个数字中不含
和;
(3)三个数字中恰好出现两次.
19.（本题8分）如图，三个元件
安置在线路中，各个元件发生故障是相互独立的，且概率分别为
、
、
.求线路由于元件发生故障而中断的概率.
 |
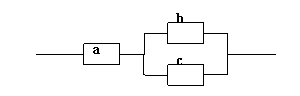20.（本题8分）在核发电站里，一台机器人负责核反应堆的若干根铀
燃料棒的自动维护管理工作.已知在小时内，每一根铀棒需要维护的概率是
.为使核电站正常工作，而机器人也管理得过来，要求在小时内，核电站的铀燃料棒，在一根以上的维护概率不超过
.问在设计这种机器人时，每台最多应维护多少根铀燃料棒?
排列、组合和概率测试卷答案
一、选择题
1.B 2.A 3.B 4.D 5.A 6.D 7.D 8.B
9.A 
，
。
10.A 函数为偶函数，要求
,
。
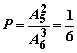二、填空题
11.20 12.14 13.4 14.
15.
三、解答题
16.有理项为第1，5，9项。
，
，
。
17.不同的任职方法数为2+3
3=11。
18.(1)
；(2)
；(3)
。
19.
。
20.
。