高二中段考试数学试题 时间:120分钟 满分:150分
试卷说明:1.答案必须填在答题卷对应的答题栏内,否则不得分.
2.交卷时只交答题卷. 3.严禁使用计算器.
一、选择题(本大题共10小题,每小题5分,共50分).在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
2. 在△ABC中,若![]() a=2bsinA,则B为( )
a=2bsinA,则B为( )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
3. 已知点(3,1)和(-4,6)在直线3x-2y+a=0的两侧,则a的取值范围是( )
A.a<-7或a>24 B.a=7或a=24
C.-7<a<24 D.-24<a<7
4. 已知等比数列![]() 的公比
的公比![]() ,则
,则![]() 等于 (
)
等于 (
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.若实数![]() 满足
满足![]() ,则
,则![]() 的最小值是( )
的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6. 若两个等差数列![]() ,
,![]() 前
前![]() 项和分别为
项和分别为![]() ,
,![]() ,满足
,满足![]() ,则
,则![]() 的值为(
)
的值为(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7. 已知不等式![]() 的解集为
的解集为![]() ,则不等式
,则不等式![]() 的解集为 (
)
的解集为 (
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.已知:在⊿ABC中,![]() ,则此三角形为( )
,则此三角形为( )
A. 直角三角形 B. 等腰直角三角形
C. 等腰三角形 D. 等腰或直角三角形
9. 等比数列![]() 的各项均为正数,且
的各项均为正数,且![]() ,则
,则![]() =( )
=( )
A. 8
B.![]() D.10
D.10
10. 设![]() 为三角形的三条边,且
为三角形的三条边,且![]() 成等差数列,则
成等差数列,则![]() 所对的角是( )。
所对的角是( )。
A.锐角 B.直角 C.钝角 D.不能确定
二、填空题(本大题共4小题,每小题5分,共20分)
11. 在△ABC中,若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
12. 在等差数列{an}中,已知公差d=![]() ,且a1+a3+a5+…+a99=60,
,且a1+a3+a5+…+a99=60,
则a1+a2+a3+…+a99+a100=____________.
13.已知1≤![]() ≤3,2≤
≤3,2≤![]() ≤4,则
≤4,则![]() 的最小值=______;最大值=_________.
的最小值=______;最大值=_________.
14.若不等式![]() 对一切
对一切![]() 恒成立,则
恒成立,则![]() 的取值范围是______________.
的取值范围是______________.
三、解答题(本大题共6小题,15、16题每题12分,17—20题每题14分,共80分)
15.(本小题满分12分)
集合![]() ,若
,若![]() ,求a的取值范围.
,求a的取值范围.
16.(本小题满分12分)
有4个数,其中前3个数成等差数列,后3个数成等比数列,并且第1个数与第4个数的和是16,第2个数与第3个数的和是12,求这4个数.
17.(本题满分14分)
△ABC的三个内角A、B、C对边分别是a, b,
c,且![]() ,
,![]() ,又△ABC的面积为
,又△ABC的面积为![]() .
.
求:(1)角C; (2)a+b的值.
18.(本小题满分14分)
深圳某商场为使销售空调和冰箱获得的总利润达到最大,对即将出售的空调和冰箱相关数据进行调查,得出下表:
| 资金 | 每台空调或冰箱所需资金(百元) | 月资金供应数量 (百元) | |
| 空调 | 冰箱 | ||
| 成本 | 30 | 20 | 300 |
| 工人工资 | 5 | 10 | 110 |
| 每台利润 | 6 | 8 | |
问:该商场怎样确定空调或冰箱的月供应量,才能使总利润最大?最大利润是多少?
19.(本小题满分14分)
我炮兵阵地位于地面A处,两观察所分别位于地面点C和D处,已知CD=
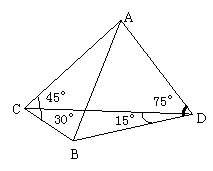 ∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°∠BDC=15°(如图)求:炮兵阵地到目标的距离.
∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°∠BDC=15°(如图)求:炮兵阵地到目标的距离.
20.(本小题满分14分)
设数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,求
,求![]() 的前6项和
的前6项和![]() ;
;
(3)若![]() ,证明
,证明![]() 是等差数列.
是等差数列.
 高二中段考试数学答题卷
高二中段考试数学答题卷
一、选择题答题栏(10×5分=50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题答题栏(4×5分=20分)
11、_______________ 12、_______________
13、_______________ 14、_______________
三、解答题答题栏(80分)
 15、(12分)
15、(12分)
 16、(12分)
16、(12分)

17、(14分)
 18、(14分)
18、(14分)
 19、(14分)
19、(14分)

20、(14分)
高二中段考试数学试题答案及评分标准
一、选择题.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | C | C | B | B | C | B | C | D | A |
二、填空题
11、 ![]() ; 12、 145 ; 13、 3,
; 12、 145 ; 13、 3, ![]() ; 14、
; 14、![]()
15、![]()
![]() ……………………2分
……………………2分
![]() ……………………………………………………2分
……………………………………………………2分
![]() ………………………………3分
………………………………3分
根据题意可得: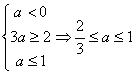 ………………5分
………………5分
16、设这4个数分别为![]() ,………………………………2 分
,………………………………2 分
依题意得: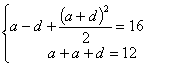 ……………………………………4分
……………………………………4分
整理得:a=4或a=9
所以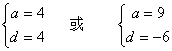 ……………………………………4分
……………………………………4分
所以这4个数分别是0,4,8,16或15,9,3,1. ………………………2分
17、(1)由已知:![]()
![]() ……6分
……6分
(2)![]() ……………………2分
……………………2分
又![]()
![]() ………………………………………4分
………………………………………4分
![]() ……2分
……2分
18、设空调和冰箱的月供应量分别为![]() 台,月总利润为
台,月总利润为![]() 百元…………………1分
百元…………………1分
则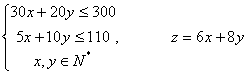 ……………………………………3分
……………………………………3分
作出可行域 ……………………………………………………………………………3分
![]() ,纵截距为
,纵截距为![]() ,斜率为k=
,斜率为k=![]() ,满足
,满足
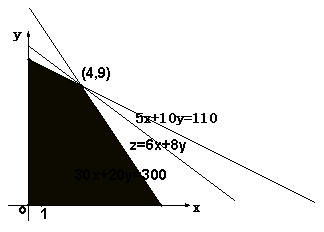 欲
欲![]() 最大,必
最大,必![]() 最大,此时,直线
最大,此时,直线![]() 必过图形
必过图形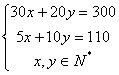
的一个交点(4,9),![]() 分别为4,9 …………………………………………………………………………4分
分别为4,9 …………………………………………………………………………4分
此时,z=6x+8y=96(百元) …………………………………………………………2分
∴空调和冰箱的月供应量分别为4、9台时,月总利润最大
最大值为9600元. ……………………………………………1分
19.解:在△ACD中,![]()
根据正弦定理有:![]()
同理:在△BCD中,![]()
![]() ,
,
根据正弦定理有:![]()
在△ABD中,![]()
根据勾股定理有:![]()
所以:炮兵阵地到目标的距离为![]() 。
。
20.解(1)![]()
![]()
![]()
![]()
![]() 即
即![]()
![]() 是公比为2的等比数列,且
是公比为2的等比数列,且![]() ………………………3分
………………………3分
![]() 即
即![]()
![]()
![]()
![]() ………………………………………………5分
………………………………………………5分
(2)![]() ,
,![]()
![]()
![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列…………………8分
的等比数列…………………8分
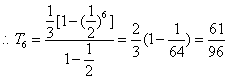 …………………10分
…………………10分
(3)![]()
![]()
即![]()
![]() 是等差数列……………………………………14分
是等差数列……………………………………14分